математика
 Вряд ли можно найти в окружающем нас мире объект, о котором известно еще меньше, чем известно людям о черных дырах. Черные дыры в нашем понимании — это самые черные и самые плотные космические объекты, гравитационной ловушки которых не могут избежать даже невесомые фотоны света. Влиянием черных дыр ученые объясняют некоторые явления, которые происходят в центрах массивных галактик, а самим черным дырам ученые приписывают массу самых экзотических свойств. И недавно, в результате совместной работы ученых-физиков и ученых-математиков, черные дыры обрели еще одно свойство — оказывается, они попросту не могут существовать в реальном мире.
Вряд ли можно найти в окружающем нас мире объект, о котором известно еще меньше, чем известно людям о черных дырах. Черные дыры в нашем понимании — это самые черные и самые плотные космические объекты, гравитационной ловушки которых не могут избежать даже невесомые фотоны света. Влиянием черных дыр ученые объясняют некоторые явления, которые происходят в центрах массивных галактик, а самим черным дырам ученые приписывают массу самых экзотических свойств. И недавно, в результате совместной работы ученых-физиков и ученых-математиков, черные дыры обрели еще одно свойство — оказывается, они попросту не могут существовать в реальном мире.
Лаура Мерсини-Хаутон (Laura Mersini-Houghton), профессор физики из университета Северной Каролины в Чапел Хилле, соединив в единое целое две противоречащих на первый взгляд теории, вывела математические доказательства тому, что черные дыры не могут возникнуть и существовать в том виде, в котором об этом принято думать. Такое положение дел может вынудить ученых пересмотреть все известные современные тории о строении пространственно-временного континуума и заново разработать теорию, описывающую происхождение Вселенной.
«Мы сами находимся в шоке от того, что нам удалось выяснить» — рассказывает профессор Мерсини-Хаутон, — «Мы занимались исследованиями данной проблем более 50 лет, и все это время такие исследования служили причиной возникновения большего числа новых вопросов, чем они давали ответов на уже существующие вопросы».
В течение многих десятилетий ученые считали, что черные дыры формировались, когда сверхмассивные звезды, жизненный цикл которых подошел к концу, начинали разрушать сами себя при помощи собственной гравитации. Под влиянием этой гравитации материя звезды начинала уплотняться и в какой-то момент этот процесс приобретает лавинообразный характер, в результате чего вся звезда схлопывалась в сингулярность, в объект очень малого размера, обладающий огромной плотностью материи и, следовательно, массой. Гравитация этой сингулярности обуславливает возникновение границы, горизонта событий, вернуться из-за которого не может ни материя, ни излучение.
Понятие черной дыры столь причудливо из-за того, что в нем складываются две противоречивые фундаментальные теории. Теория гравитации Эйнштейна допускает формирование черных дыр, но одна из фундаментальных теорий квантовой механики определяет то, что никакая информация во Вселенной не может исчезнуть без следа. Попытки объединения этих двух теорий приводят к математической бессмыслице, известной как парадокс исчезновения информации в черной дыре.
Но исследования профессора Мерсини-Хаутон описывают совершенно новый сценарий. Она и Стивен Хокинг соглашаются с тем фактом, что когда звезда разрушается под влиянием собственной гравитации, она производит излучение, называемое излучением Хокинга. Однако, процесс излучения радиации Хокинга приводит к потере звездой своей массы, при этом, ее масса и плотность падают настолько что умирающая звезда раздувается и взрывается, и формирование черной дыры с горизонтом событий становятся невозможными.
Работа профессора Мерсини-Хаутон, которая была написана совместно с ученым-математиком Харальдом Пайффером (Harald Peiffer) из университета Торонто, опубликована в онлайн-издательстве ArXiv. В этом сборнике работ, которые не прошли еще экспертную оценку, также находятся более ранние работы Мерсини-Хаутон, которые являются своего рода основой для ее последней работы.
Профессор Мерсини-Хаутон уверена в том, что математические выводы о невозможности существования черных дыр являются достоверными и окончательными. Тем не менее, окончательную точку в вопросе существования черных дыр может поставить лишь получение экспериментальных данных, указывающих на возможность физического существования черных дыр.
У математического обоснования невозможности возникновения сингулярности и черных дыр имеется еще одно немаловажное следствие. Множество физиков и астрономов считает, что наша Вселенная и произошла именно из сингулярности, начав свое расширение с момента Большого Взрыва. Однако, если сингулярность не существует, то ученым придется выдвинуть новую теорию о возникновении Вселенной, в которой не будет задействован Большой Взрыв, но которая сможет объяснить все явления, наблюдаемые учеными в настоящее время..
источник

Обезьяна хочет определить, из окна какого самого низкого этажа 15-этажного дома нужно бросить кокосовый орех, чтобы он разбился. Сколько бросков потребуется обезьяне, чтобы гарантированно удовлетворить свое любопытство, если у нее есть два ореха (орехи одинаковые по своим ударопрочным характеристикам)?
Подсказка 1
Сколько бросков потребовалось бы обезьяне, если бы у нее был только один орех?
Подсказка 2
А сколько бросков обезьяне нужно, если в доме всего один этаж? Два этажа? Три этажа? Четыре этажа?
источник

В отрывке из новой книги «Наша математическая Вселенная» профессор Массачусетского технологического института (MIT) Макс Тегмарк рассматривает вопрос о том, что математика не просто описывает Вселенную, а порождает ее.
Как ответить на вопрос о сущности жизни, Вселенной и т. п.? В юмористическом фантастическом романе Дугласа Адамса «Автостопом по Галактике» («The Hitchhiker’s Guide to the Galaxy») компьютер выдал ответ в виде цифры: «42». Однако сложнее всего найти правильный ответ. Понимаю, Дуглас Адамс пошутил. Но и он не станет отрицать, что математика внесла огромный вклад в раскрытие тайн Вселенной.
Бозон Хиггса предсказан все тем же инструментом, что и планета Нептун, и радиоволны — при помощи математики. Как известно, Галилей заявил, что Вселенная является «великой книгой», написанной на языке математики. Почему же наша Вселенная кажется нам столь математичной? Как это понимать? В моей новой книге «Наша математическая Вселенная» я разъясняю, что Вселенная не просто описывается при помощи математики, но она сама и есть математика в том смысле, что все мы представляем собой элементы гигантского математического объекта, который в свою очередь является частью мультивселенной — столь гигантской, что по сравнению с ней остальные мультивселенные, о которых говорили в последние годы, выглядят малыми.
Кругом одна математика!
О какой такой математике мы собираемся говорить? О математике, изучающей лишь числа? Оглянитесь вокруг себя, и вы, наверное, сможете увидеть где-нибудь небольшое количество каких-нибудь цифр (скажем, номера страниц в свежем выпуске журнала «Scientific American»), но эти цифры — всего лишь символы, придуманные и напечатанные людьми, поэтому когда мы говорим о том, что Вселенная по своей сути является математическим объектом, то мы, конечно же, не эти цифры имеем в виду.
Многие люди приравнивают математику к арифметике — здесь сказывается влияние нашей системы образования. Однако, вопреки распространенному мнению, математики изучают и другие абстрактные структуры, гораздо более разнообразные, чем числа, — в том числе и геометрические объекты. Например, нас постоянно окружает множество всяких геометрических фигур и тел, не так ли? (Вещи, созданные человеком, типа моей книги в виде параллелепипеда, здесь мы в расчет не берем.) Бросьте камешек параллельно земле, и вы увидите, сколь совершенна линия траектории, созданная природой! Траектории брошенных тел представляют собой разновидности перевернутой параболы.
Зададим еще один вопрос: по какой орбите движутся космические тела? И здесь мы обнаружим разные виды одной и той же фигуры — эллипса. Интересно отметить, что парабола и эллипс родственны друг другу: если большую ось эллипса сильно вытянуть, то эллипс все больше и больше будет стремиться к параболе; таким образом, все траектории, в приближении являются разновидностями эллипса.
Постепенно люди обнаружили множество других форм и фигур, проявлявших себя в природе не только во время движения или под действием силы тяжести, но и при изучении других явлений — электричества, магнетизма, света, теплоты, химических процессов, радиоактивности и субатомных частиц. Именно эти формы как раз и воплощены в законах физики, которые можно описать с помощью математических уравнений так же, как мы описываем форму эллипса.
Уравнения — не единственные проявления математики. Помимо них есть еще и числа.
В данном случае я говорю не о цифрах — человеческих изобретениях (типа номеров страниц, проставленных в этой книге), а о числах, которые отражают основные свойства нашей физической реальности. Например, сколько нужно взять карандашей и расположить их таким образом, чтобы они были перпендикулярны, т. е. под углом 90 градусов друг другу? — Три карандаша. Посмотрите, например, на любой угол в своей квартире, и там вы также увидите три ребра при вершине. Откуда взялось именно число три? Мы называем это число размерностью нашего пространства, но почему она равна именно трем, а не четырем или двум или сорока двум? И почему во Вселенной существует, насколько мы можем судить, ровно шесть видов кварков? Кроме того, при описании природы мы также используем числа, называемые десятичными, когда, например, говорим, что «протон в 1836,15267 раз тяжелее электрона». Всего из 32 таких чисел физики могут получить и любую другую физическую константу из тех, которые когда-либо были найдены.
Вселенной свойственна некая математичность, которая проявляется тем больше, чем глубже человек проникает во Вселенную. Словом, как же быть со всеми этими проявлениями математики в окружающем нас физическом мире? Большинство моих коллег-физиков всего лишь ограничиваются выводом, что природа по какой-то причине описывается на языке математики, по крайней мере приблизительно. Но я убежден, что надо идти дальше. Интересно, найдете ли вы в моей теории больше смысла, чем тот профессор, который сказал, что она погубит мою научную карьеру?
Гипотеза о математической Вселенной
Я был очарован этой математичностью мироздания еще будучи аспирантом. Как-то вечером 1990-го года в Беркли, когда я вместе со своим другом Биллом Пуарье сидел и рассуждал о природе вещей, мне вдруг пришла в голову мысль: окружающая нас реальность не просто описывается математикой — она сама является математикой, правда в очень специфическом смысле; причем я говорю не о некоторых сторонах реальности, но о всей реальности целиком, включая человека.
Мое первоначальное предположение — т. е. гипотеза об окружающей нас реальности — формулировалось так: существует внешняя физическая реальность, которая совершенно не зависит от человека. Когда мы из какой-нибудь теории выводим некие умозрительные конструкции, то для удобства обозначения приходится вводить новые понятия и слова, например, «протон», «атом», «молекула», «клетка», «звезда» и т. д. Необходимо помнить, что все эти понятия созданы людьми, однако, в принципе, все может быть описано и без субъективного влияния человека.
Но если предположить, что реальность существует независимо от человека, то для ее полного описания понадобится также помощь и внеземных существ или суперкомпьютеров, которым не ведомы наши научные концепции. Так возникла гипотеза о математической Вселенной, которая утверждает, что внешняя физическая реальность является математической структурой.
Представим, что вы захотели, например, описать траекторию полета победного баскетбольного мяча, запущенного игроком за несколько секунд до окончания игры. Поскольку мяч состоит из элементарных частиц (кварков и электронов), то, в принципе, можно описать траекторию каждой частицы без ссылки на траекторию баскетбольного мяча, например, так:
частица № 1 движется по параболе;
частица № 2 движется по параболе;
…
Частица № 138314159265358979323846264 движется по параболе.
Конечно, такой способ описания движения каждой из частиц мяча крайне непрактичен, ведь чтобы описать траектории всех частиц понадобится времени больше, чем возраст Вселенной. Но этого и не нужно делать, поскольку можно рассматривать не каждую частицу в отдельности, а их совокупность, которая двигается как единое целое — именно для обозначения этого единого целого люди изобрели слово «мяч», что позволяет нам сэкономить время и в дальнейшем описывать движение всей совокупности частиц целиком.
Мяч изобретен человеком, но сказанное выше точно так же относится и к другим природным объектам, таким как молекулы, скалы, звезды — этим объектам мы даем названия для экономии времени, а также для того, чтобы нагляднее представить себе эти явления природы. Слова-обозначения полезны, однако мы даем их по своему собственному усмотрению и произволу.
И здесь возникает вопрос: а возможно ли вообще найти такое описание окружающего нас мира, которое бы не зависело от нашего субъективного мнения? Если оно возможно, тогда получится, что описание объектов окружающего мира и отношений между ними окажется полностью абстрактным, а любые слова и символы превратятся в простые этикетки-указатели, не зависящие от мнения человека. В таком случае отношения между объектами и будут считаться их свойствами.
Для ответа на поставленный вопрос нужно иметь более глубокое представление о математике. По мнению специалистов-логиков, математическая структура представляет собой множество абстрактных объектов, на котором заданы отношения. Данный подход резко контрастирует с тем, как большинство из нас представляет себе математику (скажем, в виде наказания или всяких там фокусов с числами).
Итак, современная математика занимается формальным описанием структур, которые могут быть определены абстрактно, т. е. без какого-либо субъективного человеческого вмешательства. Скажем, математические символы — это всего лишь пустые этикетки без внутреннего смысла. Не имеет никакого значения, как мы записываем простую операцию сложения — словами («два плюс два равно четыре»), в виде формулы («2 + 2 = 4») или на каком-нибудь языке, например, по-испански («dos mas dos igual a cuatro»). Как именно мы будем обозначать сущность и отношения — не столь важно; мы знаем, что единственными свойствами целых чисел являются лишь те, с помощью которых обозначаются отношения между ними. Получается, что человек не изобретает математические структуры — он их обнаруживает, а потом лишь изобретает знаки для их обозначения.
Таким образом, нужно выделить два ключевых момента: 1) гипотеза об объективном существовании мира вне человека предполагает, что «теория всего» (полное описание физической реальности) не зависит от субъективного мнения человека, и 2) любой вариант объективного описания реальности представляет собой некую математическую структуру. Из этого вытекает гипотеза о математической Вселенной (т. е. что окружающая нас физическая реальность, описываемая «теорией всего», есть ни что иное как математическая структура). Словом, если вы верите в то, что существует не зависимый от человека физический мир, то вы, следовательно, должны также верить и в то, что наша физическая реальность — это математическая структура. Все в нашем мире полностью математично, в том числе и каждый человек.
Жизнь, очищенная от субъективности
Выше мы показали, как люди привносят свое субъективное мнение в описание окружающего мира. Теперь давайте посмотрим с другой стороны: каким образом математическая абстракция может раскрыть объективную сущность, очистив ее от привнесенной человеком субъективности. Рассмотрим знаменитую в шахматах «Бессмертную партию», в которой белым для достижения победы пришлось пожертвовать большим количеством фигур — обеими ладьями, слоном, ферзем, и поставить мат при помощи двух коней, слона и нескольких пешек [знаменитая «Бессмертная партия» была сыграна в 1851 г. — прим. перев.]. Когда любители шахмат называют эту партию красивой, то они имеют в виду не привлекательность игроков, шахматной доски или фигур, а более абстрактную сущность, которую можно было бы назвать абстрактной игрой, или последовательностью ходов.
Шахматы состоят из множества абстрактных объектов (различные шахматные фигуры, квадраты двух цветов на доске и т. д.), на котором заданы отношения. Например, отношение между шахматной фигурой и квадратом заключается в том, что фигура на нем стоит. Другой вид отношения: фигура ходит по определенным клеткам. Иными словами, описывать множество фигур на шахматной доске и отношения между ними можно по-разному, например, задать их на самой доске, использовать словесное описание на английском или, скажем, испанском языке или же обозначать алгебраически. Но если мы отбросим придуманные нами описания, то что же останется? Каков объект, которые они все описывают? — Ответ: «Бессмертная партия» сама по себе, шахматная партия как абстракция. Иными словами, все предпринятые нами эквивалентные описания этой партии говорят об одном и том же — об уникальной математической структуре, которая лежит в основе шахматной партии.
Гипотеза о математической Вселенной предполагает, что мы живем, так сказать, в «реляционной реальности» в том смысле, что свойства окружающего нас мира проистекают не от свойств ее конечных строительных кирпичей, но от отношений между этими кирпичами. Следовательно, окружающая нас физическая реальность не сводится к сумме своих частей, а превосходит ее в том смысле, что эта реальность может обладать множеством каких-то своих уникальных свойств, в то время как ее части не имеют внутренних свойств вообще. Получается, что окружающий нас мир не только описывается с помощью математики, но он сам и есть математика. Опираясь на этот несколько безумный вывод, мы получаем, что люди — это части гигантского математического объекта, обладающие самосознанием. Вследствие сказанного, как я утверждаю в книге, снижается статус таких известных нам понятий, как «случайность», «сложность» и даже переоценивается понятие «иллюзии». Теперь можно предположить существование невиданных ранее параллельных вселенных, настолько обширных и необычных, что по сравнению с ними все вышеупомянутые странные вселенные бледнеют, вынуждая нас отказаться от многих наших наиболее глубоких представлений о реальности.
Когда сталкиваешься с такой гигантской реальностью, то чувствуешь себя маленьким и беспомощным. Люди испытывали подобные чувства и раньше, когда вдруг узнавали, что окружавший их конечный мир на самом деле является лишь небольшой частью более крупной структуры — так было в случае с нашей планетой и Солнечной системой, нашей Галактикой и Вселенной, а, возможно, и всей иерархией параллельных вселенных, вложенных одна в другую по типу русских матрешек. Тем не менее в этом подходе я также вижу большой потенциал, поскольку мы постоянно недооцениваем не только размеры нашей Вселенной, но и мощь человеческого разума, способного ее разгадать. У наших предков, живших в пещерах, объем головного мозга был такой же как и у нас, а поскольку они не сидели по вечерам у телевизоров, то у них, конечно, было время задаться такими, например, вопросами: «Что это за штуки светятся там, на небе?» или «Откуда все это на небе взялось?» Для объяснения они придумали красивые мифы и байки, но им так и не удалось понять, что для получения ответов на эти вопросы главный инструмент находился в них самих. И для того, чтобы изучать небесные объекты, совсем не надо лететь самому в космос, — достаточно, чтобы заработал человеческий разум. Когда человеческое воображение впервые покинуло Землю и приступило к расшифровке тайн Вселенной, то делало оно это силой разума, а с помощью не ракетной тяги.
Стремление к знанию настолько меня очаровало, что я не смог ему сопротивляться и поэтому стал физиком. Я написал эту книгу, потому что хотел поделиться с читателями рассказом об этом завораживающем стремлении к открытиям, особенно в наше время, когда часто порой чувствуешь свою беспомощность. Если вы решили прочитать мою книгу, то это значит, что вы решили присоединиться ко мне и моим коллегам-физикам и заняться нашим совместным поиском.
Источник

Многие понятия покинули мир науки, и соответствующие слова стали частью повседневной речи — но, к сожалению, чаще всего их используют неправильно. Мы попросили нескольких ученых рассказать, какие научные термины, по их мнению, неправильно употребляются чаще всего. Вот десять из них.
Доказательство
Физик Шон Кэрролл стенает:
Я бы сказал, что «доказательство» — это самый неправильно понятый научный концепт. У него есть формальное толкование («логическая демонстрация того, что определенные последствия вытекают из определенных предпосылок»), и оно сильно расходится с бытовым употреблением слова, значение которого ближе к простому «свидетельство в пользу чего-либо». Между тем, что говорят ученые и что слышат обыватели, существует зазор, поскольку ученые ориентируются на более четкое определение, согласно которому наука никогда ничего не «доказывает»! Поэтому, когда нас спрашивают: «Как вы „докажете“, что люди произошли от других видов путем эволюции?» — или: «Можете ли вы „доказать“, что изменения климата вызваны деятельностью человека?», — мы обычно мнемся вместо того, чтобы просто сказать: «Конечно, можем». Тот факт, что на самом деле наука ничего не доказывает, а просто создает все более и более убедительные и понятные теории (которые тем не менее всегда можно и нужно улучшать и дополнять), — это одна из ключевых черт науки, определяющая ее успехи.
Теория
Астрофизик Дэйв Голдберг предлагает свою теорию по поводу слова «теория»:
Обычные люди (а также те, у кого есть на то идеологические причины) слышат слово «теория» и думают, что оно означает «идея» или «предположение». Но нам лучше знать. Научная теория — это целая система проверяемых и потенциально опровержимых идей; все они могут быть оспорены либо благодаря очевидным фактам, либо путем эксперимента, который можно провести. Лучшие теории (в том числе специальная теория относительности, теория квантовой механики и теория эволюции) выдержали сотню, а то и больше сотни лет постоянной критики и перепроверок — со стороны тех, кто хотел доказать, что они умнее Эйнштейна, или тех, для чьих воззрений эти теории представляли метафизическую угрозу.
Кроме всего прочего, теории изменчивы, но не до бесконечности. Они могут быть неполными, в них могут содержаться отдельные неточности, при этом теория в целом будет оставаться верной. Даже теория эволюции сильно изменилась за годы существования, но ее все еще можно узнать.
Проблема с фразой «Это всего лишь теория» — в том, что она заставляет считать, что настоящая научная теория — это какая-то мелочь. А это не так.
Квантовая неопределенность и квантовая запутанность
Голдберг добавляет, что есть и другие понятия, которые исковеркали даже больше, чем «теорию». Он имеет в виду употребление специальных физических терминов для описания духовного опыта и практик в стиле нью-эйдж:
Эта неверная трактовка — следствие использования понятий квантовой механики особой породой спиритуалистов и адептов концепции «помоги себе сам». Кратко она изложена в тошнотворном фильме «Что мы знаем?! Вниз по Кроличьей Норе». Квантовая механика, как известно, строится на измерении. Позиция наблюдателя, импульс и энергия могут вызвать непредсказуемый «коллапс волновой функции» (так, одна из моих первых колонок называлась «Насколько умным нужно быть, чтобы вызвать коллапс волновой функции?»). Но тот факт, что не все во Вселенной предопределено, не означает, что ты у руля. Удивляет (и, если честно, пугает), насколько тесно в определенных кругах связывают квантовую неопределенность и квантовую запутанность с идеей души или человеческого контроля над событиями или другими, такими же завиральными, предрассудками. В конце концов, мы состоим из квантовых частиц (протонов, нейтронов, электронов) и являемся частью квантовой Вселенной. Это круто, конечно, но только в том смысле, что физика — это вообще круто.
Врожденное против благоприобретенного
Эволюционный биолог Марлин Зак говорит:
Одна из моих любимых ошибок — это идея о том, что поведение может быть «врожденным» или «приобретенным» (и все вариации этого противопоставления). Первый вопрос, который мне обычно задают, если я заговариваю о поведении, это «генетическое» оно или нет — что само по себе уже признак непонимания, поскольку ВСЕ черты всегда являются результатом взаимодействия генов и среды. Только различие между чертами, а не черты сами по себе, могут быть генетическими или приобретенными. Например, если вы берете двух идентичных близнецов, воспитываете их в разных условиях и они делают что-то по-разному (например, говорят на разных языках), тогда различие приобретенное. Но владение французским языком, итальянским или любым другим не является полностью приобретенным, поскольку, очевидно, нужны определенные генетические условия для того, чтобы в принципе владеть даром речи.
Естественное
Биолог-синтетист Терри Джонсон ужасно устал от того, что люди неправильно понимают смысл этого слова:
«Естественный» и «натуральный» — это слова, которые используются в таком количестве контекстов и значений, что понять их собственный смысл представляется почти невозможным. Их самое банальное употребление — разграничение явлений, которые существуют только благодаря деятельности человека, и тех, которые могут возникать и без его участия. Оно предполагает, что люди каким-то образом отделены от природного мира, что наша жизнедеятельность «неестественна» по сравнению с жизнью, скажем, бобров или медоносных пчел.
Если говорить о еде, понятие «натуральный» еще более скользкое. В разных странах оно имеет разные значения. В США Управление по надзору за качеством продуктов и медикаментов махнуло рукой на осмысленное определение «натуральной еды» (в основном в пользу еще более зыбкого термина «органическая еда»). В Канаде я могу торговать кукурузой как «натуральным» продуктом, если ничего в нее не добавлял или не извлекал из нее перед продажей; однако кукуруза как таковая — это продукт длившейся тысячелетия культивации ее человеком, выведения ее из растения, которого без человеческого вмешательства не существовало бы.
Ген
Впрочем, еще больше Джонсона угнетает употребление слова «ген»:
25 ученым потребовалось два дня споров, чтобы породить следующее определение: «Ген — это локализуемый фрагмент геномной последовательности, соответствующий единице наследования, которая связывается с регулирующими, считывающими и/или другими функциональными фрагментами последовательности». Это означает, что ген — это отдельный фрагмент ДНК, на который мы можем указать и сказать: «Этот кусок за что-то отвечает или регулирует производство чего-то». Определение оставляет пространство для маневра; не так давно мы считали, что большая часть нашей ДНК вообще ничего не делает. Мы называли ее «мусорной ДНК», но вот сейчас обнаруживается, что значительная часть этого мусора обладает функциями, которые видны не с первого взгляда.
Обычно наиболее неправильное использование слова «ген» можно опознать по следующему за ним определению «для чего-то». Здесь есть две проблемы. У всех нас имеются гены для гемоглобина, но не у всех есть серповидно-клеточная анемия. У разных людей разные версии гена «для гемоглобина», называемые «аллели». Одни аллели гемоглобина связаны с развитием серповидно-клеточного заболевания, а другие — нет. Так что ген отсылает к семейству аллелей, и только некоторые члены этого семейства (если такие вообще есть) связаны с болезнями или нарушениями. Ген сам по себе не плох (поверьте, без гемоглобина вы долго не протянете), но частная версия гемоглобина, которая есть лично у вас, может вызывать проблемы.
Больше всего меня беспокоит популяризация идеи о том, что если генетическая вариация с чем-то коррелирует, то это и есть «ген для» чего-то. Подобным словоупотреблением говорящий предполагает, что «этот ген вызывает порок сердца», тогда как в реальности обычно «люди с этой аллелью более подвержены пороку сердца, но мы точно не знаем почему, и, возможно, эта аллель обладает компенсирующими преимуществами, которых мы не заметили, потому что не искали их».
Статистически значимый
Математик Джордан Элленберг хотел бы разъяснить недоразумение с этим понятием:
«Статистически значимый» — это одно из тех выражений, которые ученые хотели бы переформулировать, будь у них такая возможность. «Значимый» подразумевает важность; но тест на статистическую значимость, разработанный британским статистиком Рональдом Эйлмером Фишером, измеряет не важность или размеры какого-либо эффекта — а только то, можем ли мы, используя наши лучшие статистические инструменты, отличить его значение от нуля. «Статистически заметный» или «статистически различимый» было бы куда лучше.
Выживание наиболее приспособленного
Палеоэколог Жаклин Джилл говорит, что люди неверно трактуют одну из базовых идей теории эволюции:
Мой список возглавляет понятие «выживание наиболее приспособленного». Во-первых, сам Дарвин никогда ничего такого не утверждал. Во-вторых, люди неверно понимают выражение «наиболее приспособленный». В связи с этим сбивается и понимание эволюционного процесса в целом. Среди прочего весьма устойчива идея о том, что эволюция прогрессивна и однонаправленна (или даже предумышленна со стороны некоторых организмов, поскольку люди обычно не воспринимают идею естественного отбора). Или что все черты должны быть адаптивны (сексуальный отбор существует! и случайные мутации тоже!).
«Самый приспособленный» не значит «самый сильный» или «самый умный». Это означает «организм, лучше всего подходящий для жизни в определенной среде», и под этим может подразумеваться что угодно, в диапазоне от «самый маленький» или «самый податливый» до «самый ядовитый» или «лучше других обходящийся неделями без воды». Кроме того, живые существа не всегда эволюционируют в том направлении, которое мы могли бы объяснить адаптацией. Их эволюционный путь может быть сильнее связан со случайными мутациями или с теми чертами, которые представители их вида находят привлекательными.
Геологические мерки времени
Джилл, чьи работы посвящены изучению окружающей среды эпохи плейстоцена, существовавшей более 15 000 лет назад, говорит, что ее пугает, как мало людей понимает последовательность событий на Земле:
Проблема, с которой я часто сталкиваюсь, состоит в том, что людям не хватает понимания геологических временных рамок. Все доисторическое в сознании широких масс спрессовывается, и люди думают, что 20 000 лет назад на Земле существовали совершенно другие виды (нет!) или даже динозавры (нет! нет! нет!). Ситуацию не улучшает и то, что в упаковки с игрушечными динозаврами часто кладут пещерных людей или мамонтов.
Органический
По мнению энтомолога Гвен Пирсон, существует целая группа терминов, которые постоянно сопровождают слово «органический»: «без химикатов», «натуральный» и т. д. И ее уже воротит смотреть, насколько неправильно люди употребляют эти понятия:
Меня не столько расстраивает, что употребление этих слов формально неверно — поскольку, естественно, вся еда органическая, так как содержит углерод и т. д. Раздражает то, что они используются, чтобы свести на нет реальные различия в составе еды и в процессах производства. Что-то может быть «органическим» и при этом весьма опасным. А что-то может быть «синтетическим» и рукотворным, но безопасным, а порой и просто лучше, чем «естественное». Если вы принимаете инсулин, не исключено, что он произведен из генно-модифицированных бактерий. И по-прежнему спасает жизни.
Источник

Теория всего — гипотетическая объединённая физико-математическая теория, описывающая все известные фундаментальные взаимодействия. Первоначально данный термин использовался в ироническом ключе для обозначения разнообразных обобщённых теорий. Со временем термин закрепился в популяризациях квантовой физики для обозначения теории, которая бы объединила все четыре фундаментальные взаимодействия в природе. В научной литературе вместо термина «теория всего» используется термин «единая теория поля», тем не менее следует иметь в виду, что теория всего может быть построена и без использования полей, несмотря на то, что научный статус таких теорий может быть спорным.
В течение двадцатого века было предложено множество «теорий всего», но ни одна из них не смогла пройти экспериментальную проверку, или существуют значительные затруднения в организации экспериментальной проверки для некоторых из кандидатов. Основная проблема построения научной «теории всего» состоит в том, что квантовая механика и общая теория относительности(ОТО) имеют разные области применения. Квантовая механика в основном используется для описания микромира, а общая теория относительности применима к макромиру. СТО (Специальная теория относительности) описывает явления при больших скоростях, а ОТО является обобщением ньютоновской теории гравитации, объединяющей её со СТО и распространяющей на случай больших расстояний и больших масс. Непосредственное совмещение квантовой механики и специальной теории относительности в едином формализме (квантовой релятивистской теории поля) приводит к проблеме расходимости — отсутствия конечных результатов для экспериментально проверяемых величин.
Для решения этой проблемы используется идея перенормировки величин. Для некоторых моделей механизм перенормировок позволяет построить очень хорошо работающие теории, но добавление гравитации (то есть включение в теорию ОТО как предельного случая для малых полей и больших расстояний) приводит к расходимостям, которые убрать пока не удаётся. Хотя из этого вовсе не следует, что такая теория не может быть построена.
источник

На многих людей математика может наводить ужас. Этот список, возможно, улучшит общие знания о математических приемах и ускорит выполнение математических вычислений в уме.
1. Умножение на 11
Все мы знаем, что при умножении на 10 к числу добавляется 0, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52):
5_2
Теперь сложите два числа и запишите их посередине:
5_(5+2)_2
Таким образом, ваш ответ: 572.
Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу:
9_(9+9)_9
(9+1)_8_9
10_8_9
1089 – это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все!
252 = (2x(2+1)) & 25
2 x 3 = 6
625
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5. Это срабатывает всегда:
2682 x 5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887 x 5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435
4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9х3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58 x 4 = (58 x 2) + (58 x 2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32 x 125 все равно, что:
16 x 250 все равно, что:
8 x 500 все равно, что:
4 x 1000 = 4,000
8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, — просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195 * 2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978 * 2 = 5956
Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10: 1000
-648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

Чистая математика является в своём роде поэзией логической идеи.Альберт Эйнштейн
В данной статье мы предлагаем вам подборку простых математических приёмов, многие из которых довольно актуальны в жизни и позволяют считать быстрее.
1. Быстрое вычисление процентов
Пожалуй, в эпоху кредитов и рассрочек наиболее актуальным математическим навыком можно назвать виртуозное вычисление процентов в уме. Самым быстрым способом вычислить определённый процент от числа является умножение данного процента на это число с последующим отбрасыванием двух последних цифр в получившемся результате, ведь процент есть не что иное, как одна сотая доля.
Сколько составляют 20% от 70? 70 × 20 = 1400. Отбрасываем две цифры и получаем 14. При перестановке множителей произведение не меняется, и если вы попробуете вычислить 70% от 20, то ответ также будет 14.
Данный способ очень прост в случае с круглыми числами, но что делать, если надо посчитать, к примеру, процент от числа 72 или 29? В такой ситуации придётся пожертвовать точностью ради скорости и округлить число (в нашем примере 72 округляется до 70, а 29 до 30), после чего воспользоваться тем же приёмом с умножением и отбрасыванием двух последних цифр.
2. Быстрая проверка делимости
Можно ли поровну поделить 408 конфет между 12 детьми? Ответить на этот вопрос легко и без помощи калькулятора, если вспомнить простые признаки делимости, которые нам преподавали ещё в школе.
Число делится на 2, если его последняя цифра делится на 2.
Число делится на 3, если сумма цифр, из которых состоит число, делится на 3. Например, возьмём число 501, представим его как 5 + 0 + 1 = 6. 6 делится на 3, а значит, и само число 501 делится на 3.
Число делится на 4, если число, образованное его последними двумя цифрами, делится на 4. Например, берём 2 340. Последние две цифры образуют число 40, которое делится на 4.
Число делится на 5, если его последняя цифра 0 или 5.
Число делится на 6, если оно делится на 2 и 3.
Число делится на 9, если сумма цифр, из которых состоит число, делится на 9. Например, возьмём число 6 390, представим его как 6 + 3 + 9 + 0 = 18. 18 делится на 9, а значит, и само число 6 390 делится на 9.
Число делится на 12, если оно делится на 3 и 4.
3. Быстрое вычисление квадратного корня
Квадратный корень из 4 равен 2. Это посчитает любой. А как насчёт квадратного корня из 85?
Для быстрого приблизительного решения находим ближайшее к заданному квадратное число, в данном случае это 81 = 9^2.
Теперь находим следующий ближайший квадрат. В данном случае это 100 = 10^2.
Корень квадратный из 85 находится где-то в интервале между 9 и 10, а поскольку 85 ближе к 81, чем к 100, то квадратный корень этого числа будет 9 с чем-то.
4. Быстрое вычисление времени, через которое денежный вклад под определённый процент удвоится
Хотите быстро узнать время, которое потребуется, чтобы ваш денежный вклад с определённой процентной ставкой удвоился? Тут также не нужен калькулятор, достаточно знать «правило 72».
Делим число 72 на нашу процентную ставку, после чего получаем приблизительный срок, через который вклад удвоится.
Если вклад сделан под 5% годовых, то потребуется 14 с небольшим лет, чтобы он удвоился.
Почему именно 72 (иногда берут 70 или 69) ? Как это работает? На эти вопросы развёрнуто ответит «Википедия».
5. Быстрое вычисление времени, через которое денежный вклад под определённый процент утроится
В данном случае процентная ставка по вкладу должна стать делителем числа 115.
Если вклад сделан под 5% годовых, то потребуется 23 года, чтобы он утроился.
6. Быстрое вычисление почасовой ставки
Представьте, что вы проходите собеседования с двумя работодателями, которые не называют оклад в привычном формате «рублей в месяц», а говорят о годовых окладах и почасовой оплате. Как быстро посчитать, где платят больше? Там, где годовой оклад составляет 360 000 рублей, или там, где платят 200 рублей в час?
Для расчёта оплаты одного часа работы при озвучивании годового оклада необходимо отбросить от названной суммы три последних знака, после чего разделить получившееся число на 2.
360 000 превращается в 360 ÷ 2 = 180 рублей в час. При прочих равных условиях получается, что второе предложение лучше.
7. Продвинутая математика на пальцах
Ваши пальцы способны на гораздо большее, нежели простые операции сложения и вычитания.
С помощью пальцев можно легко умножать на 9, если вы вдруг забыли таблицу умножения.
Пронумеруем пальцы на руках слева направо от 1 до 10.
Если мы хотим умножить 9 на 5, то загибаем пятый палец слева.
Теперь смотрим на руки. Получается четыре несогнутых пальца до согнутого. Они обозначают десятки. И пять несогнутых пальцев после согнутого. Они обозначают единицы. Ответ: 45.
Если мы хотим умножить 9 на 6, то загибаем шестой палец слева. Получим пять несогнутых пальцев до согнутого пальца и четыре после. Ответ: 54.
Таким образом можно воспроизвести весь столбик умножения на 9.
8. Быстрое умножение на 4
Существует чрезвычайно лёгкий способ молниеносного умножения даже больших чисел на 4. Для этого достаточно разложить операцию на два действия, умножив искомое число на 2, а затем ещё раз на 2.
Посмотрите сами. Умножить 1 223 сразу на 4 в уме сможет не каждый. А теперь делаем 1223 × 2 = 2446 и далее 2446 × 2 = 4892. Так гораздо проще.
9. Быстрое определение необходимого минимума
Представьте, что вы проходите серию из пяти тестов, для успешной сдачи которых вам необходим минимальный балл 92. Остался последний тест, а по предыдущим результаты таковы: 81, 98, 90, 93. Как вычислить необходимый минимум, который нужно получить в последнем тесте?
Для этого считаем, сколько баллов мы недобрали/перебрали в уже пройденных тестах, обозначая недобор отрицательными числами, а результаты с запасом — положительными.
Итак, 81 − 92 = −11; 98 − 92 = 6; 90 − 92 = −2; 93 − 92 = 1.
Сложив эти числа, получаем корректировку для необходимого минимума: −11 + 6 − 2 + 1 = −6.
Получается дефицит в 6 баллов, а значит, необходимый минимум увеличивается: 92 + 6 = 98. Дела плохи. 🙁
10. Быстрое представление значения обыкновенной дроби
Примерное значение обыкновенной дроби можно очень быстро представить в виде десятичной дроби, если предварительно приводить её к простым и понятным соотношениям: 1/4,1/3, 1/2 и 3/4.
К примеру, у нас есть дробь 28/77, что очень близко к 28/84 = 1/3, но поскольку мы увеличили знаменатель, то изначальное число будет несколько больше, то есть чуть больше, чем 0,33.
11. Трюк с угадыванием цифры
Можно немного поиграть в Дэвида Блэйна и удивить друзей интересным, но очень простым математическим трюком.
Попросите друга загадать любое целое число.
Пусть он умножит его на 2.
Затем прибавит к получившемуся числу 9.
Теперь пусть отнимет 3 от получившегося числа.
А теперь пусть разделит получившееся число пополам (оно в любом случае разделится без остатка).
Наконец, попросите его вычесть из получившегося числа то число, которое он загадал в начале.
Ответ всегда будет 3.
Да, очень тупо, но часто эффект превосходит все ожидания.
Бонус
И, конечно же, мы не могли не вставить в этот пост ту самую картинку с очень крутым способом умножения.

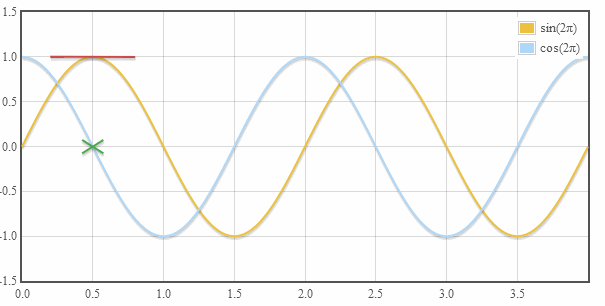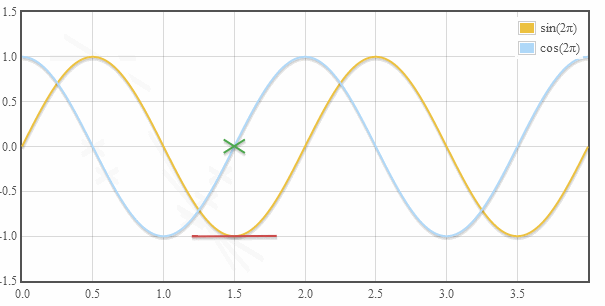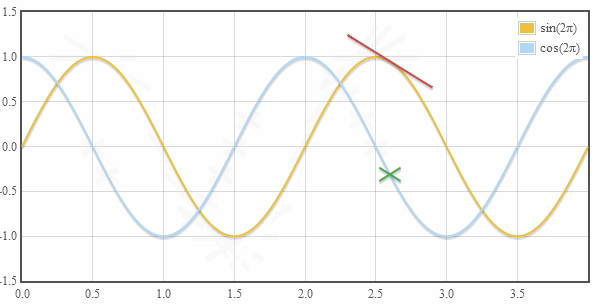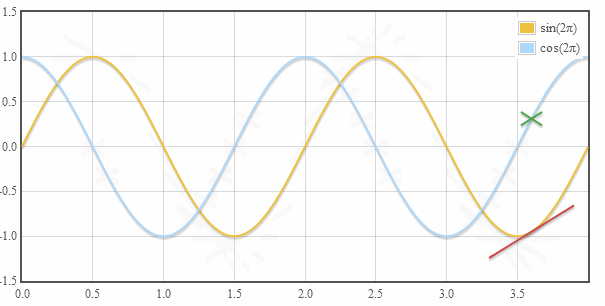
1. Синус и косинус угла
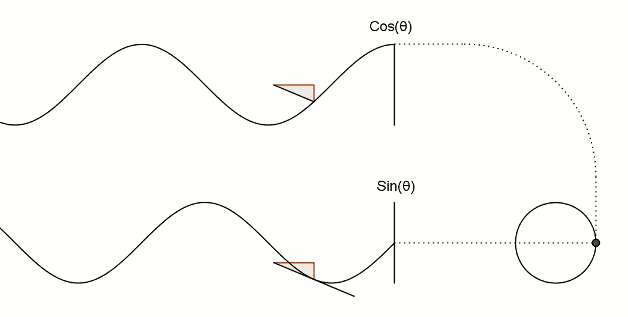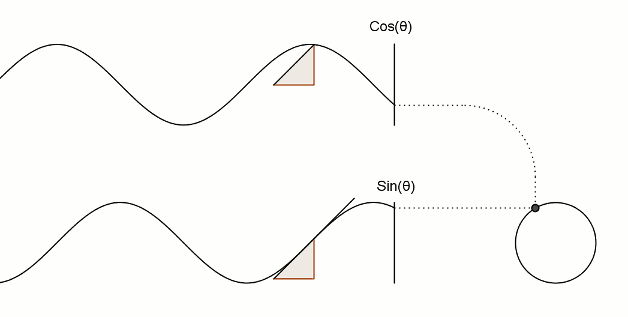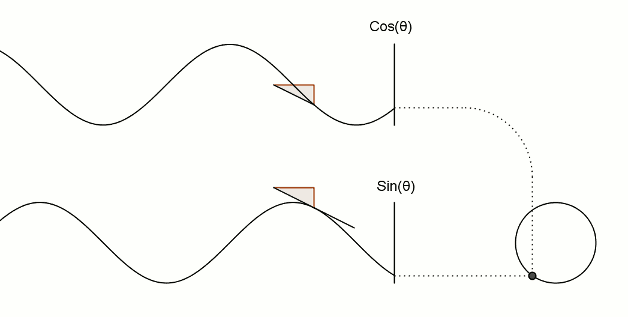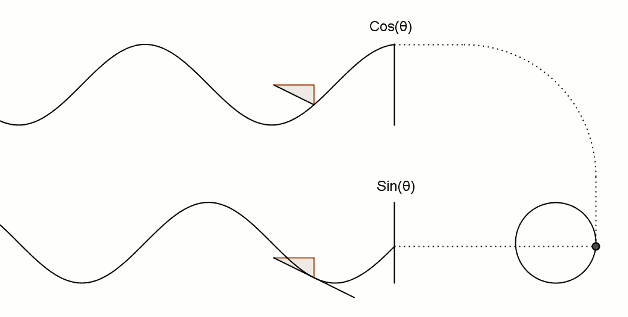
2. Косинус — производная синуса
3. Еще одна визуализация тангенса
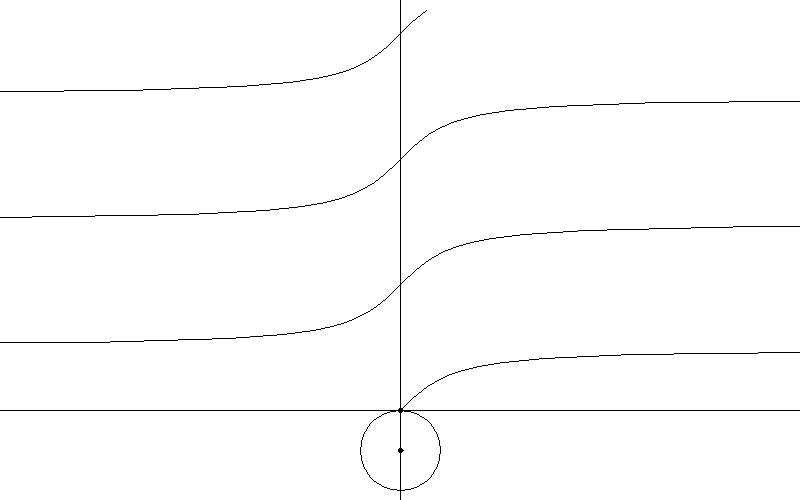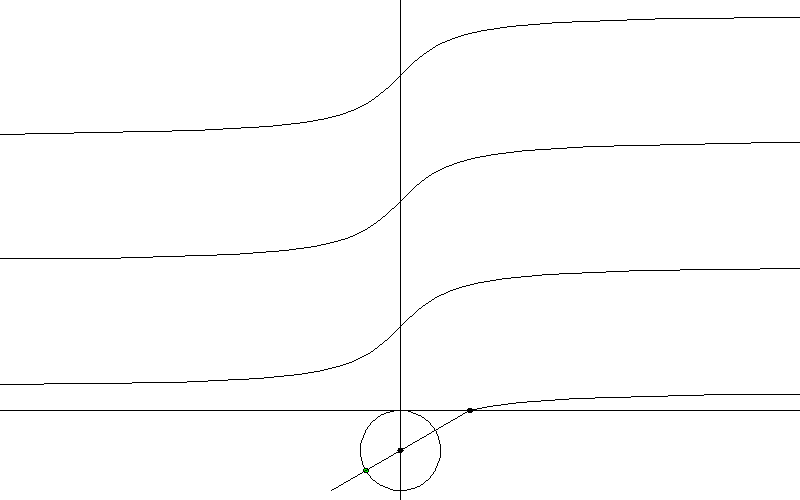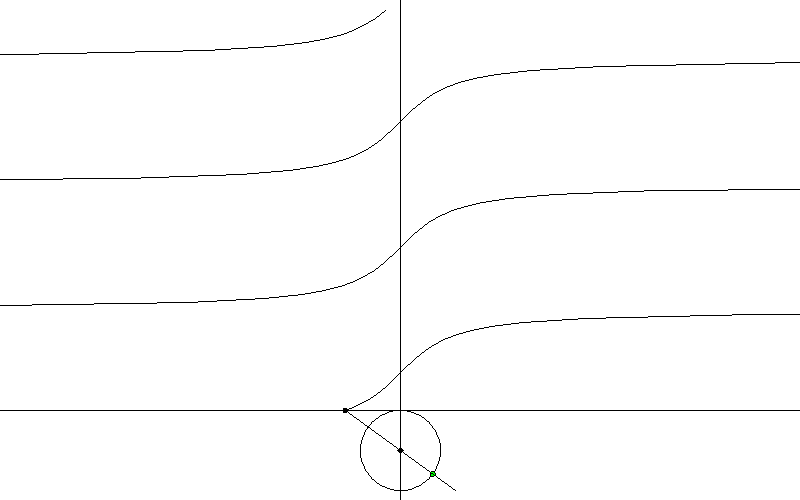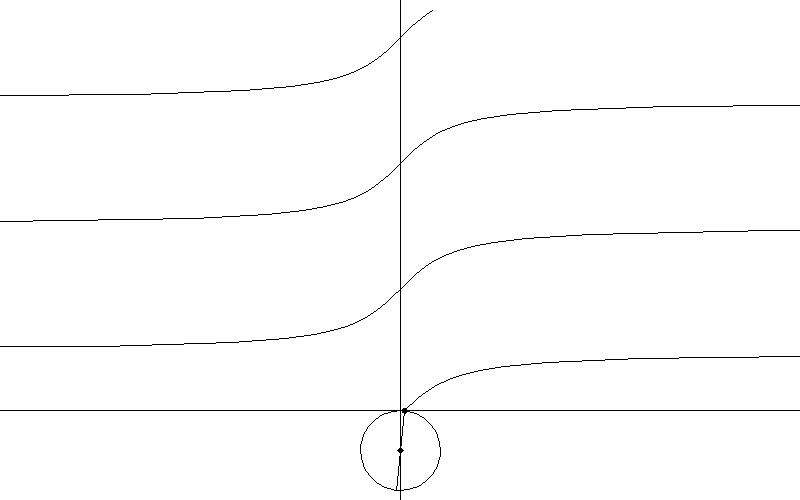
4. Перевод функции из прямоугольной в полярную систему координат
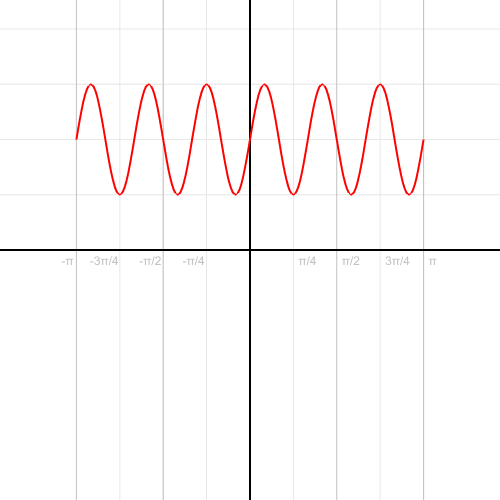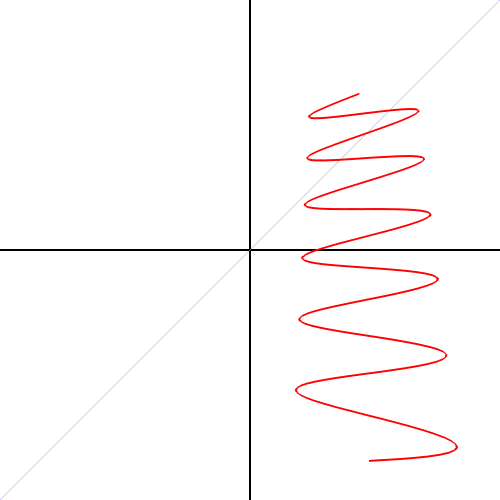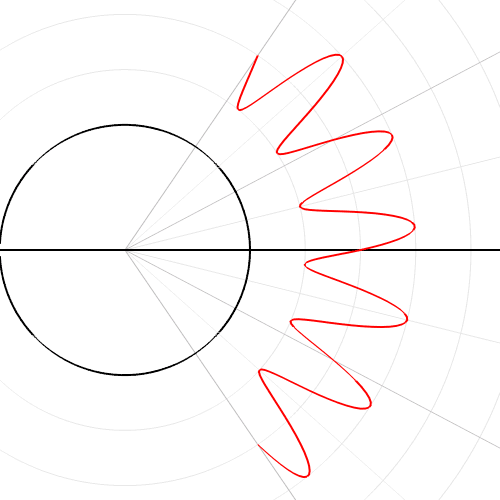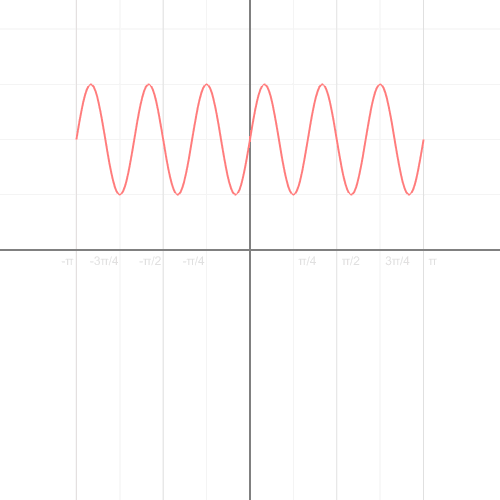
5. Рисование параболы
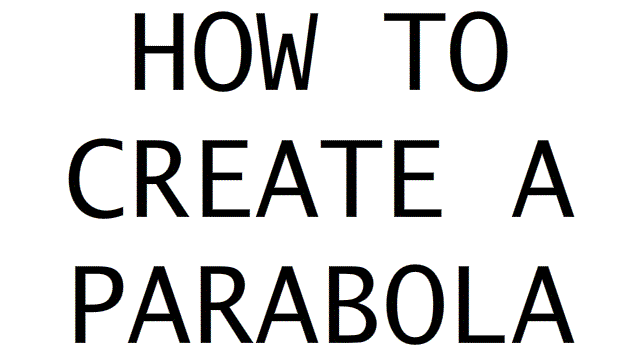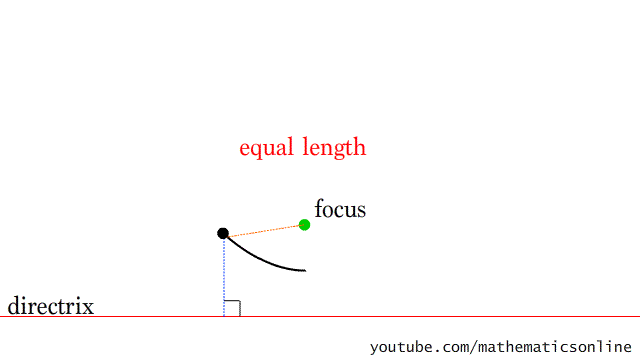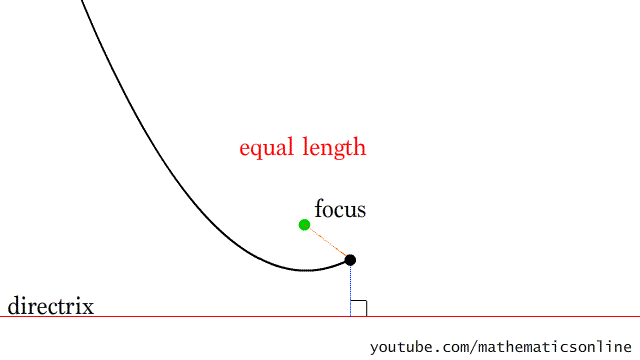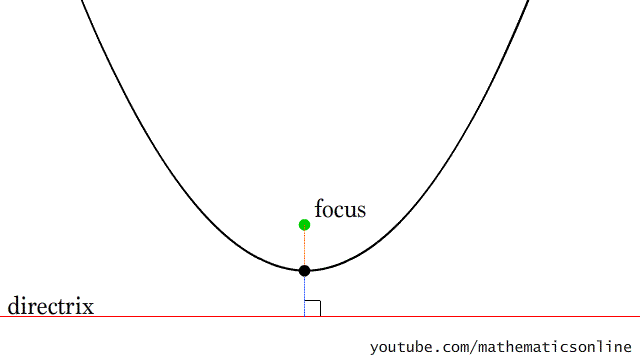
6. Сумма Римана
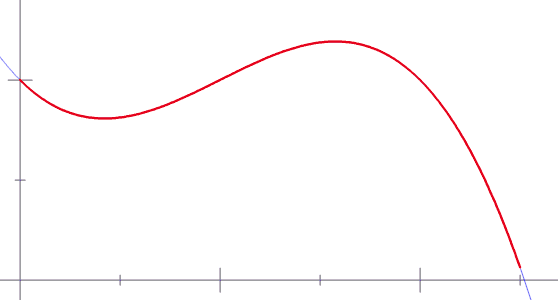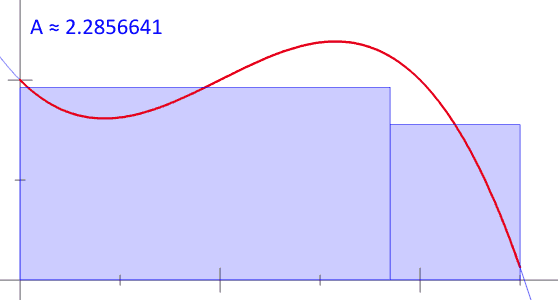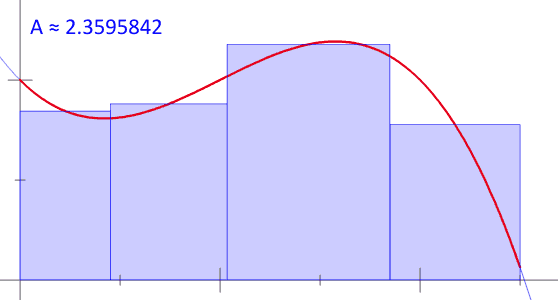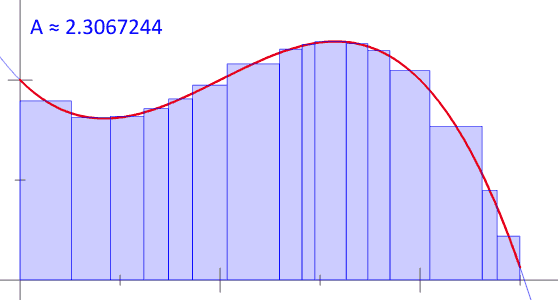
7. Гипербола

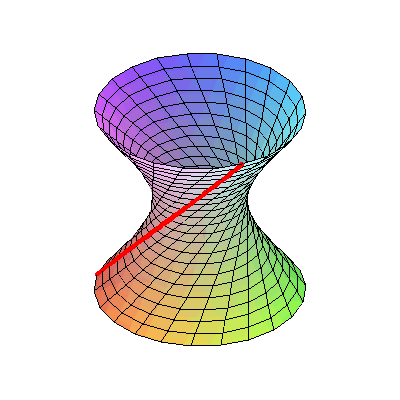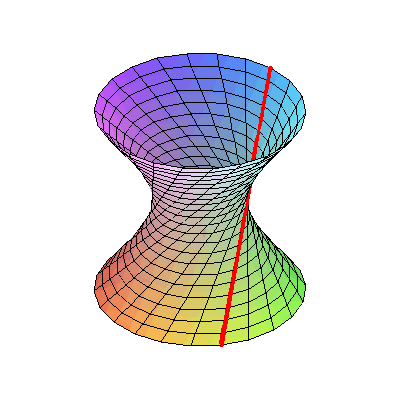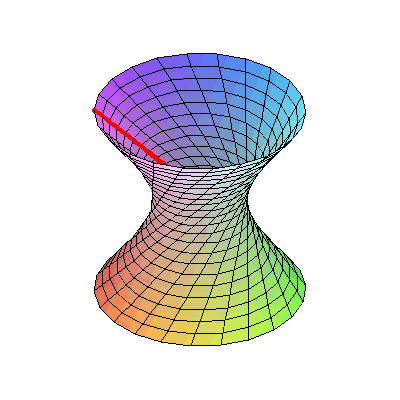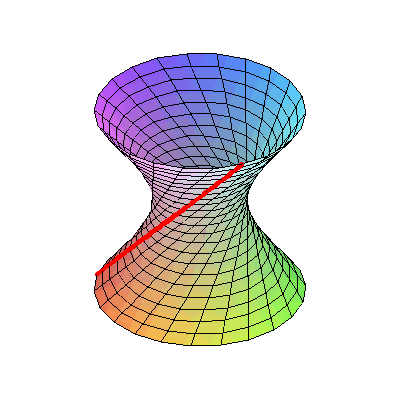
8. Гиперболоид
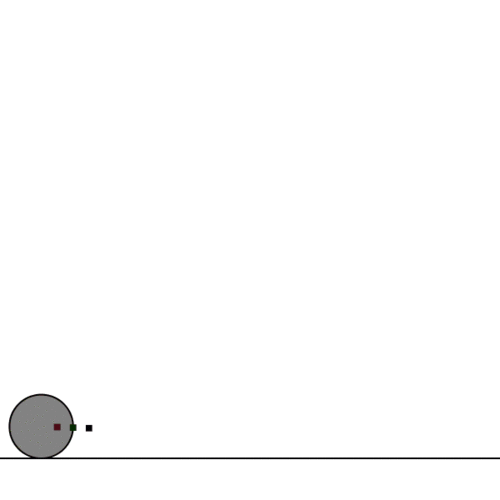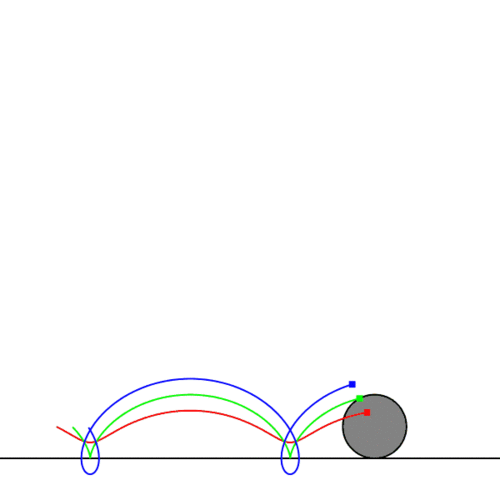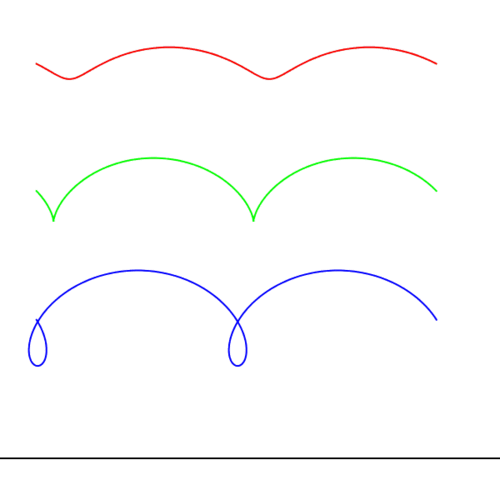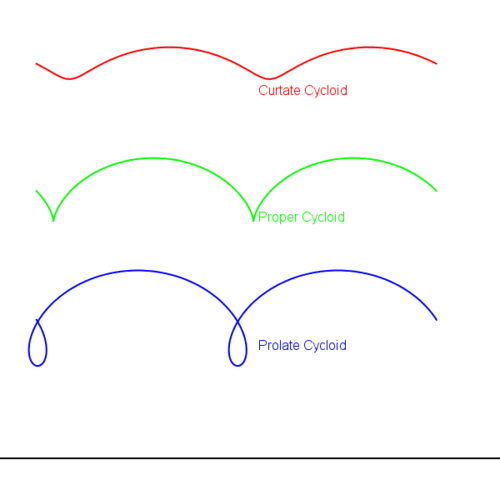
9. Циклоиды

Этот список нескольких малоизвестных математических трюков покажет вам как быстро считать в уме в случаях, посложнее чем 5 умножить на 10, а ещё ваши знакомые смогут пользоваться вами, как калькулятором.
1. Умножаем на 11
Все мы знаем, как быстро умножить число на 10, нужно лишь добавить ноль в конце, но знаете ли вы, что есть фишка как легко умножить двузначное число на 11?
Допустим, нам нужно умножить 63 на 11. Возьмите двузначное число, которое нужно умножить на 11 и представьте между его двумя цифрами место:
6_3
Теперь сложите первую и вторую цифру этого числа и поместите в это место:
6_(6+3)_3
И наш результат умножения готов:
63*11=693
Если же результат сложения первой и второй цифры двузначное число, вставляйте только вторую цифру, а к первой цифре исходного числа прибавляйте единицу:
79*11=
7_(7+9)_9
(7+1)_6_9
79*11=869
2. Быстрое возведение в квадрат числа, оканчивающегося на 5
Если вам нужно возвести в кадрат двузначное число, заканчивающееся на 5, то вы можете сделать это очень просто в уме. Умножьте первую цифру числа на саму себя плюс единица и добавьте в конце 25, и это всё:
45*45=4*(4+1)_25=2025
3. Умножение на 5
Для большинства людей умножение на 5 не составляет труда для небольших чисел, но как быстро считать в уме большие числа, умноженные на 5?
Вам нужно взять это число и разделить на 2. Если результат целое число, то добавьте к нему 0 в конце, если нет, отбросьте остаток и добавьте 5 в конце:
1248*5=(1248/2)_(0 или 5)=624_(0 или 5)=6240 (результат деления на 2 целое число)
4469*5=(4469/2)_(0 или 5)=(2234.5)_(0 или 5)=22345 (результат деления на 2 число с остатком)
4. Умножение на 4
Это очень простая и, с первого взгляда, очевидная фишка умножения любого числа на 4, но насмотря на это люди не догадываются о ней в нужный момент. Чтобы просто умножить любое число на 4, нужно уножить его на 2, а потом снова умножить на 2:
67*4=67*2*2=134*2=268
Вы уверенны что выбрали правильную профессию? »>
5. Вычислить 15%
Если вам нужно в уме вычислить 15% от какого-либо числа, то есть простой способ, как это сделать. Возьмите 10% от числа (разделив число на 10) и добавьте к этому числу половину от полученных 10%.
15% от 884 рублей=(10% от 884 рублей)+((10% от 884 рублей)/2)=88.4 рубля + 44.2 рубля = 132.6 рублей
6. Умножение больших чисел
Если вам нужно перемножить большие числа в уме и одно из них четное, то вы можете воспользоваться методом упрощения множителей, уменьшя четно число в два раза, а второе увеличивая в два раза:
32*125 это
16*250 это
8*500 это
4*1000=4000
7. Деление на 5
Разделить большое число на 5 в голове очень просто. Всё что нужно, это умножить число на 2 и сместить запятую на один знак назад:
175/5
Умножаем на 2: 175*2=350
Смещаем на один знак: 35.0 или 35
1244/5
Умножаем на 2: 1244*2=2488
Смещаем на один знак: 248.8
8. Вычитание из 1000
Чтобы вычесть большое число из тысячи, следуйте простой технике, отнимайте все цифры числа от 9, кроме последней, а последнее цифру числа отнимите от 10:
1000-489=(9-4)_(9-8)_(10-9)=511
Разумеется, чтобы научиться быстро считать в уме, нужно много раз попрактиковаться в использовании этих приемов, чтобы довести их до автоматизма, одноразовое прочтение оставит только нули в вашей голове.
Для большинства людей умножение на 5 не составляет труда для небольших чисел, но как быстро считать в уме большие числа, умноженные на 5?

На многих людей математика может наводить ужас. Этот список, возможно, улучшит общие знания о математических приемах и ускорит выполнение математических вычислений в уме.
1. Умножение на 11
Все мы знаем, что при умножении на 10 к числу добавляется 0, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52):
5_2
Теперь сложите два числа и запишите их посередине:
5_(5+2)_2
Таким образом, ваш ответ: 572.
Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу:
9_(9+9)_9
(9+1)_8_9
10_8_9
1089 – это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и все!
252 = (2x(2+1)) & 25
2 x 3 = 6
625
3. Умножение на 5
Большинство людей очень просто запоминает таблицу умножения на 5, но, когда приходится иметь дело с большими числами, сделать это становится сложнее. Или нет? Этот прием невероятно прост.
Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5. Это срабатывает всегда:
2682 x 5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887 x 5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435
4. Умножение на 9
Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9х3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ – 27.
5. Умножение на 4
Это очень простой прием, хотя очевиден лишь для некоторых. Хитрость в том, что нужно просто умножить на 2, а затем опять умножить на 2:
58 x 4 = (58 x 2) + (58 x 2) = (116) + (116) = 232
6. Подсчет чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на 10), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причем одно из них — четное, вы можете просто перегруппировать их, чтобы получить ответ:
32 x 125 все равно, что:
16 x 250 все равно, что:
8 x 500 все равно, что:
4 x 1000 = 4,000
8. Деление на 5
На самом деле делить большие числа на 5 очень просто. Все, что нужно, — просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195 * 2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978 * 2 = 5956
Шаг2: 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом: Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10: 1000
-648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

