думать

Чистая математика является в своём роде поэзией логической идеи.
Альберт Эйнштейн
В данной статье мы предлагаем вам подборку простых математических приёмов, многие из которых довольно актуальны в жизни и позволяют считать быстрее.
1. Быстрое вычисление процентов
Пожалуй, в эпоху кредитов и рассрочек наиболее актуальным математическим навыком можно назвать виртуозное вычисление процентов в уме. Самым быстрым способом вычислить определённый процент от числа является умножение данного процента на это число с последующим отбрасыванием двух последних цифр в получившемся результате, ведь процент есть не что иное, как одна сотая доля.
Сколько составляют 20% от 70? 70 × 20 = 1400. Отбрасываем две цифры и получаем 14. При перестановке множителей произведение не меняется, и если вы попробуете вычислить 70% от 20, то ответ также будет 14.
Данный способ очень прост в случае с круглыми числами, но что делать, если надо посчитать, к примеру, процент от числа 72 или 29? В такой ситуации придётся пожертвовать точностью ради скорости и округлить число (в нашем примере 72 округляется до 70, а 29 до 30), после чего воспользоваться тем же приёмом с умножением и отбрасыванием двух последних цифр.
2. Быстрая проверка делимости
Можно ли поровну поделить 408 конфет между 12 детьми? Ответить на этот вопрос легко и без помощи калькулятора, если вспомнить простые признаки делимости, которые нам преподавали ещё в школе.
• Число делится на 2, если его последняя цифра делится на 2.
• Число делится на 3, если сумма цифр, из которых состоит число, делится на 3. Например, возьмём число 501, представим его как 5 + 0 + 1 = 6. 6 делится на 3, а значит, и само число 501 делится на 3.
• Число делится на 4, если число, образованное его последними двумя цифрами, делится на 4. Например, берём 2 340. Последние две цифры образуют число 40, которое делится на 4.
• Число делится на 5, если его последняя цифра 0 или 5.
• Число делится на 6, если оно делится на 2 и 3.
• Число делится на 9, если сумма цифр, из которых состоит число, делится на 9. Например, возьмём число 6 390, представим его как 6 + 3 + 9 + 0 = 18. 18 делится на 9, а значит, и само число 6 390 делится на 9.
• Число делится на 12, если оно делится на 3 и 4.
3. Быстрое вычисление квадратного корня
Квадратный корень из 4 равен 2. Это посчитает любой. А как насчёт квадратного корня из 85?
Для быстрого приблизительного решения находим ближайшее к заданному квадратное число, в данном случае это 81 = 9^2.
Теперь находим следующий ближайший квадрат. В данном случае это 100 = 10^2.
Корень квадратный из 81 находится где-то в интервале между 9 и 10, а поскольку 85 ближе к 81, чем к 100, то квадратный корень этого числа будет 9 с чем-то.
4. Быстрое вычисление времени, через которое денежный вклад под определённый процент удвоится
Хотите быстро узнать время, которое потребуется, чтобы ваш денежный вклад с определённой процентной ставкой удвоился? Тут также не нужен калькулятор, достаточно знать «правило 72».
Делим число 72 на нашу процентную ставку, после чего получаем приблизительный срок, через который вклад удвоится.
Если вклад сделан под 5% годовых, то потребуется 14 с небольшим лет, чтобы он удвоился.
Почему именно 72 (иногда берут 70 или 69) ? Как это работает? На эти вопросы развёрнуто ответит «Википедия».
5. Быстрое вычисление времени, через которое денежный вклад под определённый процент утроится
В данном случае процентная ставка по вкладу должна стать делителем числа 115.
Если вклад сделан под 5% годовых, то потребуется 23 года, чтобы он утроился.
6. Быстрое вычисление почасовой ставки
Представьте, что вы проходите собеседования с двумя работодателями, которые не называют оклад в привычном формате «рублей в месяц», а говорят о годовых окладах и почасовой оплате. Как быстро посчитать, где платят больше? Там, где годовой оклад составляет 360 000 рублей, или там, где платят 200 рублей в час?
Для расчёта оплаты одного часа работы при озвучивании годового оклада необходимо отбросить от названной суммы три последних знака, после чего разделить получившееся число на 2.
360 000 превращается в 360 ÷ 2 = 180 рублей в час. При прочих равных условиях получается, что второе предложение лучше.
7. Продвинутая математика на пальцах
Ваши пальцы способны на гораздо большее, нежели простые операции сложения и вычитания.
С помощью пальцев можно легко умножать на 9, если вы вдруг забыли таблицу умножения.
Пронумеруем пальцы на руках слева направо от 1 до 10.
Если мы хотим умножить 9 на 5, то загибаем пятый палец слева.
Теперь смотрим на руки. Получается четыре несогнутых пальца до согнутого. Они обозначают десятки. И пять несогнутых пальцев после согнутого. Они обозначают единицы. Ответ: 45.
Если мы хотим умножить 9 на 6, то загибаем шестой палец слева. Получим пять несогнутых пальцев до согнутого пальца и четыре после. Ответ: 54.
Таким образом можно воспроизвести весь столбик умножения на 9.
8. Быстрое умножение на 4
Существует чрезвычайно лёгкий способ молниеносного умножения даже больших чисел на 4. Для этого достаточно разложить операцию на два действия, умножив искомое число на 2, а затем ещё раз на 2.
Посмотрите сами. Умножить 1 223 сразу на 4 в уме сможет не каждый. А теперь делаем 1223 × 2 = 2446 и далее 2446 × 2 = 4892. Так гораздо проще.
9. Быстрое определение необходимого минимума
Представьте, что вы проходите серию из пяти тестов, для успешной сдачи которых вам необходим минимальный балл 92. Остался последний тест, а по предыдущим результаты таковы: 81, 98, 90, 93. Как вычислить необходимый минимум, который нужно получить в последнем тесте?
Для этого считаем, сколько баллов мы недобрали/перебрали в уже пройденных тестах, обозначая недобор отрицательными числами, а результаты с запасом — положительными.
Итак, 81 − 92 = −11; 98 − 92 = 6; 90 − 92 = −2; 93 − 92 = 1.
Сложив эти числа, получаем корректировку для необходимого минимума: −11 + 6 − 2 + 1 = −6.
Получается дефицит в 6 баллов, а значит, необходимый минимум увеличивается: 92 + 6 = 98. Дела плохи. 🙁
10. Быстрое представление значения обыкновенной дроби
Примерное значение обыкновенной дроби можно очень быстро представить в виде десятичной дроби, если предварительно приводить её к простым и понятным соотношениям: 1/4,1/3, 1/2 и 3/4.
К примеру, у нас есть дробь 28/77, что очень близко к 28/84 = 1/3, но поскольку мы увеличили знаменатель, то изначальное число будет несколько больше, то есть чуть больше, чем 0,33.
11. Трюк с угадыванием цифры
Можно немного поиграть в Дэвида Блэйна и удивить друзей интересным, но очень простым математическим трюком.
1. Попросите друга загадать любое целое число.
2. Пусть он умножит его на 2.
3. Затем прибавит к получившемуся числу 9.
4. Теперь пусть отнимет 3 от получившегося числа.
5. А теперь пусть разделит получившееся число пополам (оно в любом случае разделится без остатка).
6. Наконец, попросите его вычесть из получившегося числа то число, которое он загадал в начале.
Ответ всегда будет 3.
Источник
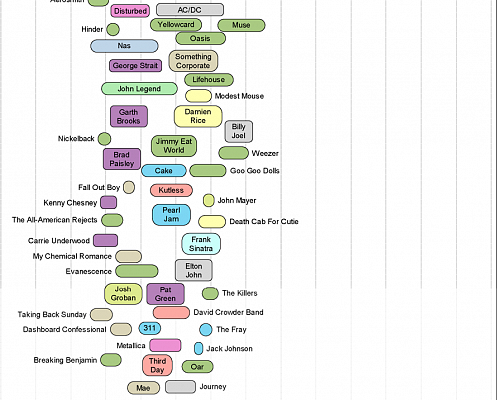 Последние несколько лет Вирджил Гриффит изучал музыкальные вкусы американских студентов с помощью Facebook. Набрав определенную статистику, он сравнил эти данные с результатами академического оценочного теста SAT, который используется при поступлении в высшие учебные заведения США.
Последние несколько лет Вирджил Гриффит изучал музыкальные вкусы американских студентов с помощью Facebook. Набрав определенную статистику, он сравнил эти данные с результатами академического оценочного теста SAT, который используется при поступлении в высшие учебные заведения США.
Возможные результаты теста лежат в диапазоне от 600 до 2400 баллов, что составляет сумму трех тестов: математика, анализ текста и грамматика, каждый из которых может дать до 800 баллов.
Например, поступившие в Калифорнийский технологический институт имеют средний балл SAT 1520, при этом из музыкальных исполнителей наибольшей популярностью у них пользуется Radiohead. Очевидно, что ее творчество можно считать музыкой для умных американских студентов.
На противоположном конце спектра расположились музыкальные предпочтения людей далеко не выдающихся способностей, и здесь мы можем видеть, к примеру, Beyoncе. Такие титаны рока, как Pink Floyd или Metallica, находятся примерно посередине — как музыка «обычных» среднестатистических студентов.
Источник
 1. Принимайте во внимание свои эмоции. Наше сознание лишь небольшая часть того, что происходит в нашей голове. В любой момент мозг обрабатывает с громадной скоростью гигантское количество информации – так быстро все осознавать мы не можем. Основываясь на своих выводах – мозг генерирует эмоции. Не игнорируйте эту тонкую подсказку – ваш личный суперкомпьютер хочет вам что-то сказать.
1. Принимайте во внимание свои эмоции. Наше сознание лишь небольшая часть того, что происходит в нашей голове. В любой момент мозг обрабатывает с громадной скоростью гигантское количество информации – так быстро все осознавать мы не можем. Основываясь на своих выводах – мозг генерирует эмоции. Не игнорируйте эту тонкую подсказку – ваш личный суперкомпьютер хочет вам что-то сказать.
2. Не думайте под нажимом обстоятельств. В моменты, когда от вас требуется только действие, уже нет смысла анализировать свои методы. «Самолет взлетел – поздно проверять запасы топлива». Один раз, затратив время на обучение мастерству (это всегда требует времени), мы в дальнейшем должны довериться своему автоматизму и выполнять действия быстро и эффективно.
3. Рассматривайте альтернативу. Этот метод часто используют игроки в покер, когда подозревают, что партнер блефует. Предположим для себя мысль, что «партнер не блефует», после этого мозг будет чутко фильтровать все признаки (речь, мимика), которые вступают в противоречие с этим фактом, принятым нами на веру.
4. Подвергайте сомнению свои привычки. Если вы любите хорошее вино – нет никакой связи между его ценой и как сильно оно понравиться лично вам. То же самое с парфюмерией, кинофильмами, книгами… Выясните, что вы лично хотите, и получайте больше удовольствия от жизни.
5. Принимайте долго душ. Исследования показывают, что часто решение проблемы приходит во время длительной прогулки или стоя под душем. Эти идеи получены на пике активности правого полушария мозга, а ум эффективнее всего работает с этим полушарием, когда он без стресса.
6. Скептически отнеситесь к своим воспоминаниям. Ученые доказали, что память человека удивительно нечестна. Сам факт воспоминания о событии меняет информацию об этом событии в нашем мозгу – меняются детали и описания. Чем больше вы думаете, тем менее достоверными становятся эти события как основа для принятия решения. Вряд ли вам стоит устраивать день рождения своего ребенка на основании воспоминаний, что же вам самому нравилось в 7 лет.
7. Не расчитывайте на идеальную фигуру и супермышление одновременно. Выяснилось, что области мозга, отвечающие за волю и мышление быстро истощаются. Простой эксперимент показал, что человек, которого попросили запомнить семизначный номер, а затем предложили поесть — между салатом и шоколадным тортом выбрал торт. А тот, кого попросили запомнить только одну цифру, без колебаний выбрал салат. В первой группе «напряжение мозга» было исчерпано. Помните, вы можете делать все, только не все сразу!
8. Работайте над ошибками. Одной общей чертой успешных людей является их желание сосредоточиться на своих промахах. Даже тогда, когда они делают хорошо, они настаивают, что могли бы делать лучше. Это, конечно, не рецепт счастья, но это жизненной важный процесс обучения, т.к. клетки мозга выясняют, как сделать правильно путем анализа, где они ошиблись.
9. Идите и мечтайте. Забудьте об эффективности. Ученые обнаружили, что мечты важнейшая составляющая творчества: они вызывают пик активности в сети мозга, которая соединяет его части и образовывает новые связи. Мечтатель в реальности делает большую работу.
10. Думайте о мышлении. Доказано, что главным залогом правильного решения является не интеллект и не опыт, а решимость найти это решение. Мозг, как армейский швейцарский нож, полон всяких инструментов. Думайте о том, какой из этих инструментов наиболее подходит для решения задачи сейчас.
источник
