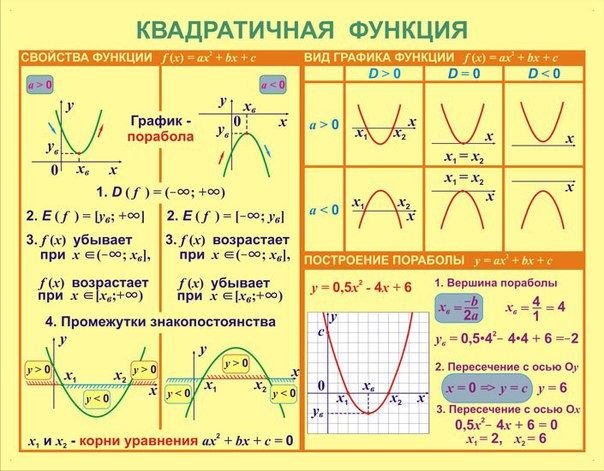
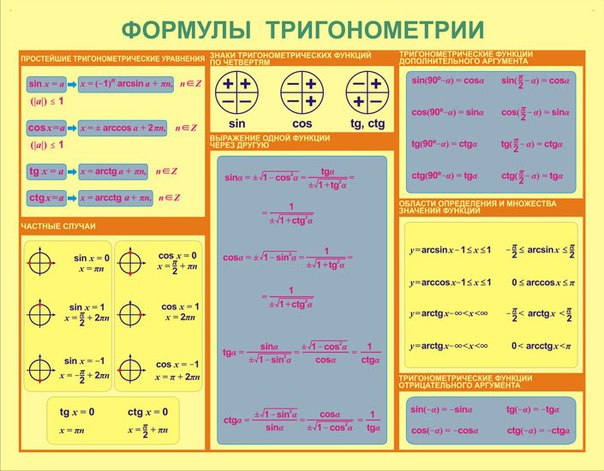
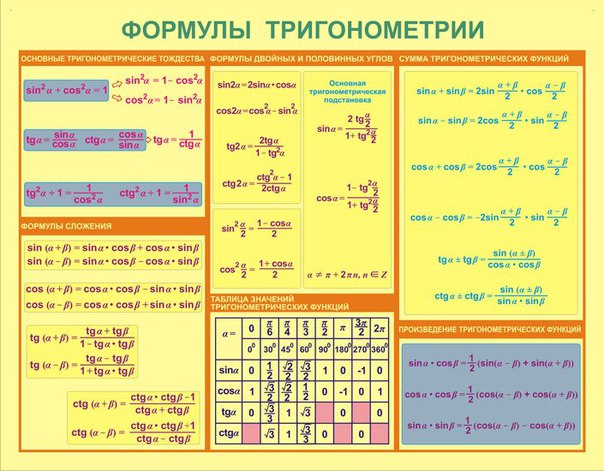
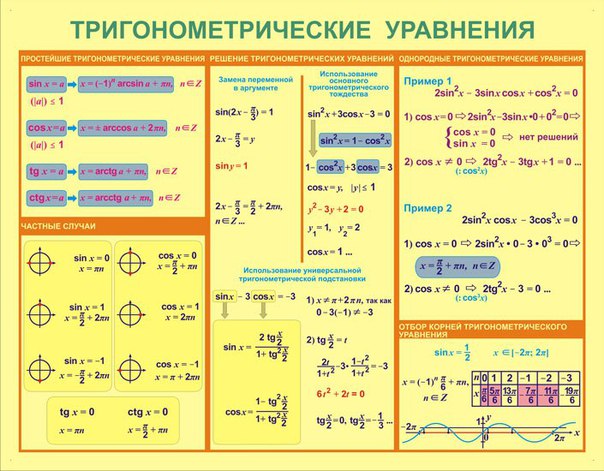
математика



Однажды преподавателю математики
Джеремми Куну задали вопрос, над которым ломал голову каждый из нас: «И где же мне пригодятся все эти ваши синусы, косинусы, интегралы и вся прочая алгебра с геометрией»? В отличии от большинства своих коллег Кун не растерялся, а назвал 5 причин, почему математика — это важно.
 На сайте «Мир фтографий» совсем недавно появилась девочка по имени Лера Лямеборшай. Ей всего 15 лет, но она уже очень способная и по-своему талантливая. Я смотрела её фотографии и они мне очень понравились — практически все без исключения! Эти снимки нравятся многим людям из «Мира фотографий», судя по их оценкам и комментариям. Эта девочка, по её словам, чтобы так фотографировать, училась 3 года. Иногда это так забирало её время, что она порой не успевала даже покушать. Но её настойчивость сыграла своё дело и её снимки хочется смотреть и смотреть… Я просто хочу здесь представить некоторые её снимки, чтобы и вы познакомились с ними и высказали своё мнение о них.
На сайте «Мир фтографий» совсем недавно появилась девочка по имени Лера Лямеборшай. Ей всего 15 лет, но она уже очень способная и по-своему талантливая. Я смотрела её фотографии и они мне очень понравились — практически все без исключения! Эти снимки нравятся многим людям из «Мира фотографий», судя по их оценкам и комментариям. Эта девочка, по её словам, чтобы так фотографировать, училась 3 года. Иногда это так забирало её время, что она порой не успевала даже покушать. Но её настойчивость сыграла своё дело и её снимки хочется смотреть и смотреть… Я просто хочу здесь представить некоторые её снимки, чтобы и вы познакомились с ними и высказали своё мнение о них.

Художник Николай Ге детально воспроизвел барочный интерьер комнаты дворца «Монплезир», побывав в ней только один раз. Секрет фотографической памяти мастера состоял, по его словам, в том, чтобы «ежедневно по памяти изображать то, что вам встречалось дорогою, будь это свет, будь это форма, будь это выражение, будь это сцена — все, что остановило ваше внимание». T&P публикуют отрывок из бестселлера Дениса Букина и издательства «Альпина Паблишер» «Развитие памяти по методикам спецслужб» о том, как использовать ассоциации, чтобы запоминать больше и лучше.
е только признанные гении обладают выдающейся памятью. В одном эксперименте испытуемым, обычным людям, показали 10 000 слайдов, после чего проверили, сколько из них запомнилось. Оказалось, что точность узнавания изображений составила около 80% — очень высокий результат. В случае, если для эксперимента выбирали необычные, яркие и красочные картины, точность узнавания повышалась практически до 100%.
Выводы:
1) Главная проблема памяти человека не в том, чтобы запомнить информацию, а в том, чтобы вспомнить и воспроизвести ее, когда это необходимо. Таким образом, задатками отличной памяти обладает каждый человек. Чтобы развить их, нужно освоить ряд приемов.
2) Мозг человека очень хорошо запоминает изображения. Поэтому большинство приемов запоминания информации — мнемотехник — основано на воображении, которое служит инструментом перевода абстрактной словесной и цифровой информации в зрительную.
Три принципа мнемотехники
Существует множество различных мнемотехник, но все они подчиняются трем принципам.
1. Использование ассоциаций
Фундаментальное свойство психики — ассоциативность. Мозг — совершенная машина для построения связей между разными образами и понятиями. Содержимое памяти представляет собой длинные, сложно организованные цепочки ассоциаций. Стоит вспомнить Рождество и Новый год, и в памяти всплывает наряженная елка, шампанское и салат оливье, запах мандаринов и поздравления. Если человек настроен на воспоминания детства, елка напомнит об утреннике в детском саду с Дедом Морозом и Снегурочкой, подарках и праздничном костюме. Прагматик погрузится в печаль от подсчета расходов. Верующий вспомнит евангельский рассказ о рождении Иисуса Христа.
Вы уже знаете, что секрет хорошей памяти состоит не столько в запоминании, сколько в извлечении информации. Запоминаемое вернее сохранится, если будет привязано к уже известному. По цепочке ассоциаций его можно будет легко вспомнить в нужный момент. Отсюда вытекает первый принцип мнемотехники: чтобы запомнить что-либо, свяжите это с тем, что хорошо вам знакомо, что вы легко можете вспомнить.
2. Кодирование информации образами
Вы уже знаете о важности воображения для хорошей памяти. Изображения запоминаются легче, чем слова и цифры. Отсюда второй принцип мнемотехники: преобразуйте в картинки то, что вам нужно запомнить. Первый и второй принципы мнемотехники используются совместно. Предположим, вам нужно в точности и надолго запомнить код автоматической ячейки камеры хранения, предназначенной для тайниковой связи: 855411. Возможно, этот код потребуется вам через несколько лет.
Представьте цифры в виде картинок (принцип кодирования через визуальные образы) и свяжите картинки воедино (принцип ассоциаций). Цифра 8 похожа на крупную женщину, 5 — на цирковой велосипед с одним колесом и рулем-сиденьем, 4 — на стул, 1 — на метлу. Женщина (8) едет на двух цирковых велосипедах (55). Одного ей мало, потому что она тяжелая. Чтобы удержать эти велосипеды вместе, она привязала их к стулу (4), на котором и сидит. Но велосипеды все-таки одноколесные, и она держит равновесие как канатоходец, с помощью двух метел (11). Едет она, конечно же, к вокзалу, в здании которого находится камера хранения. Представьте живо эту картинку, и код уже не сотрется из вашей памяти.
Маленький совет: лучше, если образы можно будет не только видеть. Они сильнее запомнятся, если будут звучать, обладать фактурой, запахом, вкусом. Вспомните Шерешевского с его синестетическим восприятием. Если вы представляете себе дерево, вообразите его в деталях: оно раскидистое, с молодой нежной листвой, пахнет свежей зеленью, с шершавой теплой корой, на которой поблескивают капельки липкой горьковатой смолы.
3. Эмоциональное отношение
Человек экономит свои силы и не любит делать лишнюю работу. Мозг выбирает приоритетные для выполнения задачи в зависимости от силы связанных с ними эмоций. Хищник, представляющий прямую угрозу, вызывает страх — с ним нужно драться или от него нужно убегать. Сильная жажда вызывает беспокойство и заставляет искать воду. Запах гнилых продуктов вызывает отвращение, которое оберегает от возможного отравления. События, связанные с сильными эмоциями, заставляют учиться: избегать троп хищников, запоминать дорогу к источнику воды, опасаться испорченных продуктов.
Эмоции активизируют память. Если попросить обычного человека назвать события, произошедшие с ним несколько лет назад, скорее всего, он вспомнит самые важные вехи своей жизни: рождение детей, встреча или расставание со спутником жизни, переезд, смену работы, яркие путешествия. Все эти события в свое время вызвали сильные эмоции и потому запомнились. Все остальное, как правило, стирается из памяти как нечто обыденное, не представляющее интереса. Иными словами, вы помните только то, что вам нужно помнить, и то, что вас действительно волнует.
Третий принцип мнемотехники: формируйте эмоциональное отношение к запоминаемой информации. Вы запомнили код ячейки камеры хранения из предыдущего пункта? Как вы думаете почему? Отчасти потому, что вас удивила или смутила абсурдность описанной комической картины женщины, едущей на одноколесных велосипедах, привязанных к стулу, и пытающейся удержать равновесие двумя метлами. Вы будете изучать мнемонические приемы. Пусть вас не смущает их абсурдность, она хороша тем, что вызывает в вас эмоции, а значит, позволяет надежно запоминать и быстро воспроизводить запомненное.
Ассоциации
Ассоциации, которые мы используем для запоминания, могут быть самыми разными.
1) Сходство по внешнему виду, функции, написанию или звучанию. Основаниями для сходства могут быть:
— цифра 8 похожа на крупную женщину, на очки или на знак бесконечности;
— самолет летает, и этим он подобен птице, парашюту и воздушному змею;
— термин «катализатор», обозначающий вещество, ускоряющее протекание химической реакции, можно запомнить с помощью слов «катал» и «затор»: после добавления катализатора реакция «катилась без заторов».
2) Противопоставление по какому-нибудь признаку: светлое и темное, соленое и сладкое, мужское и женское.
3) Отношение причины и следствия. Тучи приносят дождь. У огня становится теплее. На банановой кожуре можно поскользнуться.
4) Смежность в пространстве и времени. Кремль в Москве. Медный всадник в Санкт-Петербурге. Леонардо да Винчи и эпоха Возрождения.
Длинный плащ и шляпа устойчиво ассоциируются со шпионажем в пространстве современной культуры (хотя настоящие шпионы предпочитают не выделяться и редко носят экстравагантные плащи). История подтверждает, насколько важны ассоциации для запоминания. Многие древние тексты: эпосы, сказания, научные трактаты и сборники медицинских рецептов — были созданы в стихотворной форме. Метр, рифма, созвучия и повторы — эти ассоциации между словами помогали нашим предкам помнить наизусть огромные тексты.
В развитии памяти есть одна закономерность: чем больше человек знает, тем легче ему запоминать. Обладателю обширной системы знаний проще вплести в нее новые данные — связать их с тем, что он уже знает. Психологи иногда используют красивую метафору для описания того, как человек осваивает что-то новое. Поначалу, когда он только знакомится с предметом, он будто сажает молодое дерево. Через некоторое время саженец приживается, его корни становятся сильнее и глубже — объем знаний увеличивается, они систематизируются. Укорененный саженец может лучше питаться и быстрее расти. Человек, заложивший системную основу в изучении нового предмета, легче добавит к ней новые сведения и лучше их запомнит. Главный вывод, который нужно сделать из этого: не бойтесь браться за что-то новое. Поначалу будет трудно, но потом, когда вы освоитесь, станет легче, и вы сможете достигнуть желаемого результата. У разведчика не бывает двух одинаковых заданий.
Упражнение
Умение быстро подбирать ассоциации, связывать с их помощью самые разные вещи является неотъемлемой частью любой мнемотехники. Развить его можно постоянно практикуясь. Почаще ассоциируйте пары предметов, которые попадаются вам на глаза. Как связать дверную ручку и канцелярскую скрепку? Может быть, они схожи своей изогнутой формой? А может, вы переплавите коробку скрепок, чтобы отлить ручку? Или просто прикрепите к дверной ручке канцелярскую скрепку?
Списки слов
Умение запоминать списки слов — значимый этап в развитии памяти. Во-первых, это эффектно. Вы можете поразить друзей, повторив продиктованные вам 40 слов с первого до последнего. Во-вторых, это позволит вам запоминать список дел на день, повестку совещания, план своего выступления. Разведчик, умеющий запоминать списки слов, помнит пароли, легенды, сценарии операций, контакты нужных людей. На слова нанизываются факты, сопоставив которые можно найти связи между, казалось бы, независимыми событиями. Существует две основные техники запоминания списка слов: метод историй и метод мест. Вы освоите и сможете использовать их оба. Впрочем, возможно, вам больше понравится один из них, а с другим вы просто ознакомитесь. Решите сами.
Метод историй
К примеру, вам дан список слов:
нефть;
стол;
таксист;
кофе;
шифр;
дерево;
балкон.
История может быть такой. Вы в темной портовой таверне. Снаружи шумит море, слышны гудки кораблей и крики грузчиков. У окна стоит бочка с нефтью — ржавая железяка источает резкий, неприятный запах мазута. Бочка накрыта круглым деревянным щитом. За ней, как за столом, сидит грустный таксист в вельветовой куртке и пьет черный кофе. Он за рулем, и поэтому ром, обычный напиток таверны, ему недоступен. Запах кофе смешивается с запахом мазута. Таксист должен забрать из порта пассажира, но не может, потому что фамилия пассажира зашифрована и он не знает шифра. Таксист угрюмо смотрит на желтоватый лист с напечатанной на нем абракадаброй. Но тут вам приходит SMS-сообщение, что ключ к шифру находится на дереве у входа в таверну. В удивлении вы показываете сообщение таксисту и вместе с ним выбегаете наружу. Таксист пытается забраться на дерево, но безрезультатно — ствол гладкий и скользкий. Поэтому он поднимается на второй этаж таверны, выходит на балкон, оттуда перелезает на дерево и забирает конверт с ключом.
Представили себе историю? Теперь повторите список слов. Попробуйте сделать это в обратном порядке. Получилось? Обратите внимание, что здесь использованы все три принципа мнемотехники. Сама история представляет собой ряд ассоциаций. Слова кодируются яркими образами: ржавая вонючая бочка, мягкий вельвет, горький черный кофе, пожелтевший лист бумаги и т. д. Участники истории переживают эмоции: таксист грустит, вы удивлены неожиданным сообщением, и все заканчивается хеппи-эндом.
Упражнения
1) Запомните географию места, в котором вы живете. Если в вашем городе есть метро, запомните его карту. Каждая ветка — это список станций. Удостоверьтесь, что вы можете повторить названия станций в любом порядке. Запомните последовательно все ветки. Со временем вы сможете ориентироваться в метро исключительно по памяти. Подобным образом можно запомнить последовательность улиц, остановок автобуса и т. д. Это может оказаться полезным, когда потребуется оторваться от наружного наблюдения или воспользоваться легендой.
2) Откройте книгу на любой странице и запоминайте первое слово на каждой строке. Если вам встретился предлог, частица или часть слова, оставшаяся после переноса, возьмите второе слово. Запомните слова, закройте книгу, воспользовавшись закладкой. Воспроизведите список и проверьте себя.
Образы абстрактных понятий
Обычно не составляет проблем представить образы вещей и предметов. Говоря «чашка», вы видите свою любимую чашку, у которой есть форма, цвет и вес. «Дорога» вызовет в воображении знакомый вам участок дороги. Но что делать с абстрактными понятиями, не имеющими предметного воплощения, вроде «согласия», «обязательства» или «суггестии»? Существует два приема перекодирования таких понятий в образы. Первый основан на созвучии. Вы подбираете слово или слова, которые звучат похоже на то, которое вы хотите запомнить. Затем вы кодируете в образ именно это созвучное слово.
Второй прием использует символическое воображение: вы подбираете конкретный образ-символ интуитивно, так чтобы он выражал абстрактное понятие. Этот символ может быть общепринятым, а может быть понятным только для вас. «Со-гласие» напоминает о голосах, звучащих в унисон. Образ хора легко представить себе визуально. «Обязательство» созвучно обозу, который нужно тащить за собой как груз обязательств. «Суггестию» можно вообразить в виде высокого снежного сугроба — первых трех первых букв часто достаточно, чтобы построить ассоциацию.
Если вы хотите использовать символы, «согласие» можно вообразить как крепкое рукопожатие. Или как египетский обелиск на площади Согласия в Париже. «Обязательство» можно представить в виде официального документа с печатью. «Суггестию» может символизировать эстрадный гипнотизер в тюрбане и плаще с красной подкладкой. Ассоциации и символы очень индивидуальны. У знатока Средневековья слово «суггестия» ассоциируется с именем аббата Сугерия, жившего в XI–XII веках и известного как заказчик готического храма Сен-Дени в пригороде Парижа. Чем шире кругозор человека, тем легче ему подбирать ассоциации и запоминать новое.
Упражнение
Возьмите словарь терминов малознакомой вам области знания: техники, философии или психологии. Открывайте его наугад и подбирайте образы для встречающихся вам слов, используя фонетические и символические ассоциации.
Запоминание фраз
Способность быстро запоминать списки слов и придумывать визуальные истории открывает возможность для запоминания более крупных объемов информации, в частности, фраз и фрагментов текста. Например, вас инструктируют перед новым заданием и нужно запомнить пароль: «Захар Борисович велел передать, что краны будут на следующей неделе». Один из вариантов истории к такому паролю будет таким. Леопольд Захер-Мазох (он написал «Женщину в мехах», поэтому одет в шубу) стоит, обнявшись с первым президентом России Борисом Ельциным. Конечно, у обоих повелительный взгляд, ведь они оба наслаждались властью (правда, каждый по-своему). Захер-Мазох передает вам связку строительных кранов. Краны завернуты в график их поставки — большой лист календаря, на котором закрашена вторая строка — следующая неделя. Попробуйте теперь забыть эту фразу.
Упражнение
Придумайте визуальные истории к известным вам пословицам, поговоркам и крылатым фразам.
Запоминание иностранных слов
В разведшколах обучение иностранным языкам поставлено на поток. Для опытных преподавателей не бывает неспособных учеников. Разведчика подбирают по умственным способностям, а уж научить его свободно и без акцента говорить на любом языке — дело техники. На начальном этапе освоения языка ученику требуется запоминать пары слов, причем одно из слов известно (на родном языке), другое — нет (на иностранном). Используйте следующий алгоритм.
1) Известное слово на родном языке кодируется с помощью образа. Вам знакома эта техника по методу историй.
2) Второе, неизвестное слово проще закодировать через фонетическое сходство: подобрать одно или несколько слов на родном языке так, чтобы вместе они были созвучны иностранному.
3) Связать в одну историю образ слова на родном языке с образами слов, созвучных иностранному.
источник
В отрывке из книги «Наша математическая Вселенная» профессор Массачусетского технологического института (MIT) Макс Тегмарк рассматривает вопрос о том, что математика не просто описывает Вселенную, а порождает ее.
Как ответить на вопрос о сущности жизни, Вселенной и т.п.? В юмористическом фантастическом романе Дугласа Адамса «Автостопом по Галактике» («The Hitchhiker’s Guide to the Galaxy») компьютер выдал ответ в виде цифры: «42». Однако сложнее всего найти правильный ответ. Понимаю, Дуглас Адамс пошутил. Но и он не станет отрицать, что математика внесла огромный вклад в раскрытие тайн Вселенной.
Бозон Хиггса предсказан все тем же инструментом, что и планета Нептун, и радиоволны – при помощи математики. Как известно, Галилей заявил, что Вселенная является «великой книгой», написанной на языке математики. Почему же наша Вселенная кажется нам столь математичной? Как это понимать? В моей новой книге «Наша математическая Вселенная» я разъясняю, что Вселенная не просто описывается при помощи математики, но она сама и есть математика в том смысле, что все мы представляем собой элементы гигантского математического объекта, который в свою очередь является частью мультивселенной – столь гигантской, что по сравнению с ней остальные мультивселенные, о которых говорили в последние годы, выглядят малыми.
Кругом одна математика!
О какой такой математике мы собираемся говорить? О математике, изучающей лишь числа? Оглянитесь вокруг себя, и вы, наверное, сможете увидеть где-нибудь небольшое количество каких-нибудь цифр (скажем, номера страниц в свежем выпуске журнала «Scientific American»), но эти цифры – всего лишь символы, придуманные и напечатанные людьми, поэтому, когда мы говорим о том, что Вселенная по своей сути является математическим объектом, то мы, конечно же, не эти цифры имеем в виду.
Многие люди приравнивают математику к арифметике – здесь сказывается влияние нашей системы образования. Однако, вопреки распространенному мнению, математики изучают и другие абстрактные структуры, гораздо более разнообразные, чем числа, – в том числе и геометрические объекты. Например, нас постоянно окружает множество всяких геометрических фигур и тел, не так ли? (Вещи, созданные человеком, типа моей книги в виде параллелепипеда, здесь мы в расчет не берем.) Бросьте камешек параллельно земле, и вы увидите, сколь совершенна линия траектории, созданная природой! Траектории брошенных тел представляют собой разновидности перевернутой параболы.
Зададим еще один вопрос: по какой орбите движутся космические тела? И здесь мы обнаружим разные виды одной и той же фигуры – эллипса. Интересно отметить, что парабола и эллипс родственны друг другу: если большую ось эллипса сильно вытянуть, то эллипс все больше и больше будет стремиться к параболе; таким образом, все траектории, в приближении являются разновидностями эллипса.
Постепенно люди обнаружили множество других форм и фигур, проявлявших себя в природе не только во время движения или под действием силы тяжести, но и при изучении других явлений – электричества, магнетизма, света, теплоты, химических процессов, радиоактивности и субатомных частиц. Именно эти формы как раз и воплощены в законах физики, которые можно описать с помощью математических уравнений так же, как мы описываем форму эллипса.
Уравнения – не единственные проявления математики. Помимо них есть еще и числа.
В данном случае я говорю не о цифрах – человеческих изобретениях (типа номеров страниц, проставленных в этой книге), а о числах, которые отражают основные свойства нашей физической реальности. Например, сколько нужно взять карандашей и расположить их таким образом, чтобы они были перпендикулярны, т.е. под углом 90 градусов друг другу? – Три карандаша. Посмотрите, например, на любой угол в своей квартире, и там вы также увидите три ребра при вершине. Откуда взялось именно число три? Мы называем это число размерностью нашего пространства, но почему она равна именно трем, а не четырем или двум, или сорока двум? И почему во Вселенной существует, насколько мы можем судить, ровно шесть видов кварков? Кроме того, при описании природы мы также используем числа, называемые десятичными, когда, например, говорим, что «протон в 1836,15267 раз тяжелее электрона». Всего из 32 таких чисел физики могут получить и любую другую физическую константу из тех, которые когда-либо были найдены.
Вселенной свойственна некая математичность, которая проявляется тем больше, чем глубже человек проникает во Вселенную. Словом, как же быть со всеми этими проявлениями математики в окружающем нас физическом мире? Большинство моих коллег-физиков всего лишь ограничиваются выводом, что природа по какой-то причине описывается на языке математики, по крайней мере приблизительно. Но я убежден, что надо идти дальше. Интересно, найдете ли вы в моей теории больше смысла, чем тот профессор, который сказал, что она погубит мою научную карьеру?
Гипотеза о математической Вселенной
Я был очарован этой математичностью мироздания еще будучи аспирантом. Как-то вечером 1990-го года в Беркли, когда я вместе со своим другом Биллом Пуарье сидел и рассуждал о природе вещей, мне вдруг пришла в голову мысль: окружающая нас реальность не просто описывается математикой – она сама является математикой, правда в очень специфическом смысле; причем я говорю не о некоторых сторонах реальности, но о всей реальности целиком, включая человека.
Мое первоначальное предположение – т.е. гипотеза об окружающей нас реальности – формулировалось так: существует внешняя физическая реальность, которая совершенно не зависит от человека. Когда мы из какой-нибудь теории выводим некие умозрительные конструкции, то для удобства обозначения приходится вводить новые понятия и слова, например, «протон», «атом», «молекула», «клетка», «звезда» и т.д. Необходимо помнить, что все эти понятия созданы людьми, однако, в принципе, все может быть описано и без субъективного влияния человека.
Но если предположить, что реальность существует независимо от человека, то для ее полного описания понадобится также помощь и внеземных существ или суперкомпьютеров, которым не ведомы наши научные концепции. Так возникла гипотеза о математической Вселенной, которая утверждает, что внешняя физическая реальность является математической структурой.
Представим, что вы захотели, например, описать траекторию полета победного баскетбольного мяча, запущенного игроком за несколько секунд до окончания игры. Поскольку мяч состоит из элементарных частиц (кварков и электронов), то, в принципе, можно описать траекторию каждой частицы без ссылки на траекторию баскетбольного мяча, например, так:
частица № 1 движется по параболе;
частица №2 движется по параболе;
…
Частица № 138314159265358979323846264 движется по параболе.
Конечно, такой способ описания движения каждой из частиц мяча крайне непрактичен, ведь чтобы описать траектории всех частиц понадобится времени больше, чем возраст Вселенной. Но этого и не нужно делать, поскольку можно рассматривать не каждую частицу в отдельности, а их совокупность, которая двигается как единое целое – именно для обозначения этого единого целого люди изобрели слово «мяч», что позволяет нам сэкономить время и в дальнейшем описывать движение всей совокупности частиц целиком.
Мяч изобретен человеком, но сказанное выше точно так же относится и к другим природным объектам, таким как молекулы, скалы, звезды – этим объектам мы даем названия для экономии времени, а также для того, чтобы нагляднее представить себе эти явления природы. Слова-обозначения полезны, однако мы даем их по своему собственному усмотрению и произволу.
И здесь возникает вопрос: а возможно ли вообще найти такое описание окружающего нас мира, которое бы не зависело от нашего субъективного мнения? Если оно возможно, тогда получится, что описание объектов окружающего мира и отношений между ними окажется полностью абстрактным, а любые слова и символы превратятся в простые этикетки-указатели, не зависящие от мнения человека. В таком случае отношения между объектами и будут считаться их свойствами.
Для ответа на поставленный вопрос нужно иметь более глубокое представление о математике. По мнению специалистов-логиков, математическая структура представляет собой множество абстрактных объектов, на котором заданы отношения. Данный подход резко контрастирует с тем, как большинство из нас представляет себе математику (скажем, в виде наказания или всяких там фокусов с числами).
Итак, современная математика занимается формальным описанием структур, которые могут быть определены абстрактно, т.е. без какого-либо субъективного человеческого вмешательства. Скажем, математические символы – это всего лишь пустые этикетки без внутреннего смысла. Не имеет никакого значения, как мы записываем простую операцию сложения – словами («два плюс два равно четыре»), в виде формулы («2 + 2 = 4») или на каком-нибудь языке, например, по-испански («dos mas dos igual a cuatro»). Как именно мы будем обозначать сущность и отношения – не столь важно; мы знаем, что единственными свойствами целых чисел являются лишь те, с помощью которых обозначаются отношения между ними. Получается, что человек не изобретает математические структуры – он их обнаруживает, а потом лишь изобретает знаки для их обозначения.
Таким образом, нужно выделить два ключевых момента: 1) гипотеза об объективном существовании мира вне человека предполагает, что «теория всего» (полное описание физической реальности) не зависит от субъективного мнения человека, и 2) любой вариант объективного описания реальности представляет собой некую математическую структуру. Из этого вытекает гипотеза о математической Вселенной (т.е. что окружающая нас физическая реальность, описываемая «теорией всего», есть ни что иное как математическая структура). Словом, если вы верите в то, что существует не зависимый от человека физический мир, то вы, следовательно, должны также верить и в то, что наша физическая реальность – это математическая структура. Все в нашем мире полностью математично, в том числе и каждый человек.
Жизнь, очищенная от субъективности
Выше мы показали, как люди привносят свое субъективное мнение в описание окружающего мира. Теперь давайте посмотрим с другой стороны: каким образом математическая абстракция может раскрыть объективную сущность, очистив ее от привнесенной человеком субъективности. Рассмотрим знаменитую в шахматах «Бессмертную партию», в которой белым для достижения победы пришлось пожертвовать большим количеством фигур – обеими ладьями, слоном, ферзем, и поставить мат при помощи двух коней, слона и нескольких пешек [знаменитая «Бессмертная партия» была сыграна в 1851 г. – прим. перев.]. Когда любители шахмат называют эту партию красивой, то они имеют в виду не привлекательность игроков, шахматной доски или фигур, а более абстрактную сущность, которую можно было бы назвать абстрактной игрой, или последовательностью ходов.
Шахматы состоят из множества абстрактных объектов (различные шахматные фигуры, квадраты двух цветов на доске и т.д.), на котором заданы отношения. Например, отношение между шахматной фигурой и квадратом заключается в том, что фигура на нем стоит. Другой вид отношения: фигура ходит по определенным клеткам. Иными словами, описывать множество фигур на шахматной доске и отношения между ними можно по-разному, например, задать их на самой доске, использовать словесное описание на английском или, скажем, испанском языке или же обозначать алгебраически. Но если мы отбросим придуманные нами описания, то что же останется? Каков объект, которые они все описывают? – Ответ: «Бессмертная партия» сама по себе, шахматная партия как абстракция. Иными словами, все предпринятые нами эквивалентные описания этой партии говорят об одном и том же – об уникальной математической структуре, которая лежит в основе шахматной партии.
Гипотеза о математической Вселенной предполагает, что мы живем, так сказать, в «реляционной реальности» в том смысле, что свойства окружающего нас мира проистекают не от свойств ее конечных строительных кирпичей, но от отношений между этими кирпичами. Следовательно, окружающая нас физическая реальность не сводится к сумме своих частей, а превосходит ее в том смысле, что эта реальность может обладать множеством каких-то своих уникальных свойств, в то время как ее части не имеют внутренних свойств вообще. Получается, что окружающий нас мир не только описывается с помощью математики, но он сам и есть математика. Опираясь на этот несколько безумный вывод, мы получаем, что люди – это части гигантского математического объекта, обладающие самосознанием. Вследствие сказанного, как я утверждаю в книге, снижается статус таких известных нам понятий, как «случайность», «сложность» и даже переоценивается понятие «иллюзии». Теперь можно предположить существование невиданных ранее параллельных вселенных, настолько обширных и необычных, что по сравнению с ними все вышеупомянутые странные вселенные бледнеют, вынуждая нас отказаться от многих наших наиболее глубоких представлений о реальности.
Когда сталкиваешься с такой гигантской реальностью, то чувствуешь себя маленьким и беспомощным. Люди испытывали подобные чувства и раньше, когда вдруг узнавали, что окружавший их конечный мир на самом деле является лишь небольшой частью более крупной структуры – так было в случае с нашей планетой и Солнечной системой, нашей Галактикой и Вселенной, а, возможно, и всей иерархией параллельных вселенных, вложенных одна в другую по типу русских матрешек. Тем не менее в этом подходе я также вижу большой потенциал, поскольку мы постоянно недооцениваем не только размеры нашей Вселенной, но и мощь человеческого разума, способного ее разгадать. У наших предков, живших в пещерах, объем головного мозга был такой же, как и у нас, а поскольку они не сидели по вечерам у телевизоров, то у них, конечно, было время задаться такими, например, вопросами: «Что это за штуки светятся там, на небе?» или «Откуда все это на небе взялось?» Для объяснения они придумали красивые мифы и байки, но им так и не удалось понять, что для получения ответов на эти вопросы главный инструмент находился в них самих. И для того, чтобы изучать небесные объекты, совсем не надо лететь самому в космос, – достаточно, чтобы заработал человеческий разум. Когда человеческое воображение впервые покинуло Землю и приступило к расшифровке тайн Вселенной, то делало оно это силой разума, а с помощью не ракетной тяги.
Стремление к знанию настолько меня очаровало, что я не смог ему сопротивляться и поэтому стал физиком. Я написал эту книгу, потому что хотел поделиться с читателями рассказом об этом завораживающем стремлении к открытиям, особенно в наше время, когда часто порой чувствуешь свою беспомощность. Если вы решили прочитать мою книгу, то это значит, что вы решили присоединиться ко мне и моим коллегам-физикам и заняться нашим совместным поиском.
источник









источник










источник

Простые числа стали «менее одинокими». В доказательстве, предложенном Тан Чжан (Yitang Zhang), утверждается и показывается, что число простых чисел, имеющих «почти соседа», которое также является простым, — бесконечно много, несмотря на то, что разделять эти числа может до 70 миллионов других чисел.
Это доказательство существенно приближает математиков к решению одной из самых серьёзных и нерешенных задач, так называемой, гипотезе чисел-близнецов.
Число называется простым, если оно делится без остатка только на само себя и на единицу. Числа-близнецы — это простые числа, отличающиеся на 2, например, 3 и 5, 5 и 7 или 11 и 13.
Наибольшая известная на сегодняшний день пара чисел-близнецов: 3 756 801 695 685 × 2 666 669 + 1 и 3 756.801 695 685 × 2 666 669 — 1, которые были обнаружены в 2011 году.
Гипотеза чисел-близнецов, идея которой в 1849 году была предложена французским математиком Альфонсом де Полиньяком, утверждает, что существует бесконечное число этих пар. Несмотря на простоту своей концепции, гипотеза по сей день остается неразрешенной.
Чтобы частично упростить решение этой гипотезы была предложена другая задача: доказать, что количество конечных простых чисел, которые имеют соседние простые числа на некотором расстоянии от первого числа, даже если это расстояние гораздо больше, чем 2 — бесконечно?
«Как правило, разрыв между простыми числами увеличивается для все больших чисел, но команда Goldston показала, что всегда существуют некоторые простые числа, которые очень близки друг к другу даже в области очень больших чисел. Однако имелись существенные препятствия для использования метода Goldston непосредственно для решения проблемы бесконечного количества чисел-близнецов» говорит Тан Чжан (Yitang Zhang).
Блестящая идея
Во время пребывания в загородный дом своего друга, Чжана вдруг посетила мысль, позволившая ему добиться прогресса. Он понял, как показать, что существует бесконечное число простых пар, разделенных конечным количеством чисел.
К сожалению, для отдельных простых чисел это расстояние все еще достаточно велико: 70 000 000. В то же время, Чжан подчеркивает, что это верхняя граница расстояния.
«Это значение очень грубо, — говорит он. — Я думаю, что у меня получится уменьшить это расстояние до одного миллиона, а может, даже меньше», — и это станет ещё одним прорывом в математике и позволит ещё больше приблизиться к решению гипотезы чисел-близнецов. Важно то, что Чжан сумел показать, что разрыв между соседними простыми числами не может превышать определенного значения.
Люди будут ошеломлены результатом, математики будут работать над этой проблемой ещё очень долго.
Проблема Гольдбаха
Другой проблемой в теории простых чисел, в решении которой был достигнут некоторый прогресс, стала проблема, впервые сформулированная Гольдбахом в 1742 году. Гольдбах предположил, что каждое четное число, большее 2, является суммой двух простых чисел. Гаральд Хельфготт из Высшей школы в Париже предложил решение частного случая: нечетные Гольдбаха выше 5 являются суммой трех простых чисел.
Доказательство «частного случая» гипотезы Гольдбаха свидетельствует о том, что вы можете взять четное число, состоящее из двух простых чисел, и прибавить к нему 3, чтобы получить нечетное число, составив его, таким образом, из трех простых чисел. «Но доказательство Хельфготт вряд ли поможет математикам продвинуться в правильном направлении», — говорит Теренс Тао из Калифорнийского университета — то есть проблема Гольдбаха осталась нерешенной.
источник

Даже если вы ничего не понимаете в математике, даже если в школе ненавидели этот предмет, даже если считаете себя чистым гуманитарием… В общем, в любом случае — эти факты вам понравятся.
1. Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.
2. Религиозные евреи стараются избегать христианской символики и, вообще, знаков, похожих на крест. Например, ученики некоторых израильских школ вместо знака «плюс» пишут знак, повторяющий перевёрнутую букву «т».
3. Подлинность купюры евро можно проверить по её серийному номеру буквы и одиннадцати цифр. Нужно заменить букву на её порядковый номер в английском алфавите, сложить это число с остальными, затем складывать цифры результата, пока не получим одну цифру. Если эта цифра — 8, то купюра подлинная.
Ещё один способ проверки заключается в подобном складывании цифр, но без буквы. Результат из одной буквы и цифры должен соответствовать определённой стране, так как евро печатают в разных странах. Например, для Германии это X2.
4. Бытует мнение, что Альфред Нобель не включил математику в список дисциплин своей премии из-за того, что его жена изменила ему с математиком. На самом деле Нобель никогда не был женат.
Настоящая причина игнорирования математики Нобелем неизвестна, но есть несколько предположений. Например, на тот момент уже существовала премия по математике от шведского короля. Другое — математики не делают важных изобретений для человечества, так как эта наука имеет чисто теоретический характер.
5. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса a с центрами в вершинах равностороннего треугольника со стороной a. Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия (с неточностью в 2%).
6. В русской математической литературе ноль не является натуральным числом, а в западной, наоборот, принадлежит ко множеству натуральных чисел.
7. Американский математик Джордж Данциг, будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.
8. Сумма всех чисел на рулетке в казино равняется «числу зверя» — 666.
9. Софья Ковалевская познакомилась с математикой в раннем детстве, когда на её комнату не хватило обоев, вместо которых были наклеены листы с лекциями Остроградского о дифференциальном и интегральном исчислении.
10. В штате Индиана в 1897 году был выпущен билль, законодательно устанавливающий значение числа Пи равным 3,2. Данный билль не стал законом благодаря своевременному вмешательству профессора университета.
источник