математика
Умножьте 37 037 на любую цифру от 1 до 9, а затем умножьте полученную сумму на 3. Получится весьма интересный результат.


В 2003 году российский математик Григорий Перельман доказал гипотезу Пуанкаре – задачу, которой более 100 лет и которая заключалась в том, что любая фигура без отверстия может быть превращена в сферу. Перельман, считающийся одним из самых умных людей в мире, опубликовал два доказательства теоремы в 2002 и 2003 годах. Проверить его доказательство удалось команде математиков только к 2010 году. Задача была одной из семи Задач Тысячелетия Математического института Клэя в Кембридже.
Приз за доказательство любой из этих задач составляет 1 миллион долларов и Филдсовскую медаль, эквивалентную Нобелевской премии в математике. Неплохо, правда? Однако, сразу после того, как ему предложили приз, Перельман отказался от него. Гений отказался от приза, утверждая, что знания, которые он получил, стоят больше, чем финансовое поощрение.
«Я не заинтересован в деньгах или известности», — сказал Перельман. «Пустота везде и может быть подсчитана, что даёт нам удивительные возможности. Я знаю, как управлять Вселенной. Так скажите мне, зачем мне бежать за миллионом?», — сказал он в интервью местной газете. 45-летний гений до сих пор ведёт скромное существование вместе со своей матерью и сестрой в родном городе Санкт-Петербурге.
Математик Дмитрий Ветров о машинном обучении, третьем поколении нейронных сетей и компьютерном зрении

В настоящее время теория и практика машинного обучения переживают настоящую «глубинную революцию», вызванную успешным применением методов deep learning, представляющих собой третье поколение нейронных сетей. В отличие от классических (второго поколения) нейронных сетей 80–90-х годов прошлого века, новые парадигмы обучения позволили избавиться от ряда проблем, которые сдерживали распространение и успешное применение традиционных нейронных сетей. Сети, обученные с помощью алгоритмов глубинного обучения, не просто превзошли по точности лучшие альтернативные подходы, но и в ряде задач проявили зачатки понимания смысла подаваемой информации (например, при распознавании изображений, анализе текстовой информации и так далее). Наиболее успешные современные промышленные методы компьютерного зрения и распознавания речи построены на использовании глубинных сетей, а гиганты IT-индустрии, такие как Apple, Google, Facebook, скупают коллективы исследователей, занимающихся глубинным обучением целыми лабораториями.
Стоит отдельно заметить, что нейронные сети (даже третьего поколения, такие как сверточные сети, авто-кодировщики, глубинные машины Больцмана) не имеют ничего общего с биологическими нейронами, кроме названия. Поэтому говорить о том, что нейронные сети моделируют работу мозга, некорректно. Ни модель элементарного блока обработки информации (нейрона), ни алгоритмы обучения, ни структура сети в нейронных сетях не соответствуют тому, что наблюдается в биологическом мозге. Общности между мозгом и нейронными сетями не больше, чем между птицами и насекомыми: и те и другие летают, и те и другие имеют крылья, но в остальном это совершенно разные виды. Вряд ли кому-то придет в голову моделировать стрижа с помощью мухи. По сути, разговоры о том, что нейронные сети, используемые в машинном обучении, являются упрощенной моделью мозга, — это маркетинговый ход, направленный на получение учеными новых грантов.
В недавно опубликованной статье «Интригующие свойства нейронных сетей», на первый взгляд, получено два удивительных результата. Во-первых, вопреки распространенному мнению показано, что выходы отдельных нейронов имеют не больше смысла, чем случайная комбинация выходов нейронов с одного слоя. Во-вторых, у популярных архитектур нейронных сетей, используемых для классификации изображений, обнаружены «слепые пятна»: достаточно внести неуловимое глазом изменение в правильно классифицируемое изображение, и нейронная сеть начинает грубо ошибаться на модифицированной картинке. Разберем более подробно каждый из двух тезисов, озвученных в статье.
В 2012 году на главной мировой конференции по машинному обучению сотрудники корпорации Google представили нейронную сеть, обученную на базе фотографий flickr, показавшую рекордные результаты по точности классификации фотореалистичных изображений. Среди прочего было отмечено, что выходы некоторых нейронов допускали интерпретацию и являлись высокоуровневыми фильтрами, дававшими отклик на лица людей, морды котов и так далее. На этом основании ряд наблюдателей сделали вывод о том, что отдельные нейроны в нейронной сети способны выучивать разнотипные закономерности в данных, настраиваясь каждый на свой тип закономерности. На самом деле в современных алгоритмах обучения нейронных сетей нигде не используется факт индивидуальной настройки отдельных нейронов на закономерности определенного рода. Более того, такая интерпретируемая «специализация» никак в ходе обучения сети не поощряется, поэтому трудно ожидать, что отдельные нейроны окажутся более специфичны, чем случайная комбинация их выходов. При передаче сигнала по нейронной сети на вход каждому нейрону очередного слоя подается линейная комбинация выходов нейронов с предыдущего слоя, что примерно соответствует эксперименту, проведенному авторами статьи, в котором они брали случайные линейные комбинации выходов нейронов одного слоя. Более того, в работах последних лет, например, по так называемым экстремально рандомизированным случайным лесам (extremely randomized random forest), было показано, что применение случайных пороговых решающих правил к большому количеству случайных линейных комбинаций признаков объекта дает результаты, близкие к результатам, полученным после применения продвинутых и трудоемких методов машинного обучения. Главное, чтобы обучающая выборка была большого размера и линейных комбинаций было достаточно много. Так что полученный авторами статьи результат можно рассматривать как некоторый аналог того, что было получено несколькими годами ранее для случайных лесов. Поскольку нейронная сеть всегда использует линейные комбинации выходов нейронов, нет никаких оснований ожидать, что разнотипные закономерности будут «расщепляться» по отдельным нейронам: никакого информационного выигрыша от этого не будет. Разумеется, можно попробовать модифицировать процедуру обучения, добавив туда явное требование расщепления по нейронам (например, применив вариации метода независимых компонент), но это уже совсем другая история.
Второй тезис статьи имеет более серьезные последствия. Авторы убедительно показывают, что корректно обученные нейронные сети, показывающие прекрасные результаты на валидационной выборке (то есть не страдающие от эффекта переобучения), стремительно деградируют при неуловимом для глаза изменении картинки. На первый взгляд кажется, что это приговор современным нейронным сетям, но только на первый. Сразу возникает много вопросов. Если нейронные сети так катастрофически неустойчивы, то почему же они так успешно применялись (и применяются) на практике? Авторы статьи приводят примеры изменений, которым они подвергали исходные изображения, чтобы получить те, которые неправильно опознаются нейронной сетью. Можно заметить, что эти изменения, мягко говоря, нефотореалистичны и приводят к тому, что соседние пиксели картинки начинают мелко, но часто флуктуировать. Глаз этого не замечает, но вот нейронная сеть ни разу не сталкивалась с такими флуктуациями при обучении. Представьте, что, учась узнавать свиней, вы просмотрели миллион примеров розовых поросят, а в тестовой выборке увидели черного поросенка. Смогли бы вы его правильно идентифицировать и осознать, что это пример того класса, среди миллиона объектов которого вы ни разу не увидели черного поросенка, и весь миллион был розовым? Мелкая, незаметная глазу «рябь» очень хорошо заметна сверточной сети, которая не может соотнести полученное изображение с теми примерами, которые встречались на обучении, так как ни на одном из них этой ряби не было (а если бы была, то не деградировала бы на таких объектах). Вывод прост. Несмотря на то, что взгляд не улавливает различий, различия между искаженным и исходным изображениями огромны. Исходное изображение фотореалистично, а искаженное практически никогда не может быть получено камерой без последующей искусственной обработки. И в этом отношении нейронная сеть дает нам верный сигнал: это не настоящая фотография, а результат некоторой искусственной нетипичной постобработки. Где глаз обманется, нейронная сеть обмануть себя не даст. Таким образом, за нейронные сети можно быть спокойными. Если мы радикально (пусть и незаметно для глаза) не изменим входные данные, они будут давать надежные результаты.
К сожалению, не все так безоблачно. Можно представить себе и иную ситуацию. Зная принципы работы нейронной сети, входные данные можно исказить так, что она перестанет делать то, для чего она предназначена. Представьте себе, что злоумышленник, подключившись к камере наблюдения, соединенной с нейронной сетью, автоматически распознающей людей, слегка искажает сигнал, и нейронная сеть перестает опознавать людей просто потому, что она никогда с таким искажением не сталкивалась. При этом оператор, который периодически проверяет сигнал с камеры, никакой подмены не замечает. Самое неприятное заключается в том, что это «не лечится» путем расширения обучающей выборки. Доучивание нейронной сети на искажения одного рода не дает гарантии против искажений, по-прежнему неуловимых для глаза, другого рода, все же перебрать невозможно: слишком велико их многообразие. С другой стороны, теоретически возможно разработать более робастные методы путем загрубления процедур обучения, не позволяя им использовать закономерности, разрушающиеся при неуловимых изменениях картинки. В этом смысле настоящая статья сослужила хорошую службу, обратив внимание научного сообщества на необходимость доработки существующих алгоритмов глубинного обучения. Думаю, в ближайшие годы таковые методы появятся, и, как минимум, для фотореалистических изображений эту брешь удастся заделать, прежде чем глубинные сети заменят людей в системах видеонаблюдения.

Дмитрий Ветров
кандидат физико-математических наук, руководитель исследовательской группы байесовских методов, начальник департамента больших данных и информационного поиска факультета компьютерных наук НИУ ВШЭ.
материал с postnauka.ru

Что ещё отличает гениального человека? Рассмотрим на примере выдающегося французского математика Эвариста Галуа, проложившего, несмотря на короткую жизнь, новое направление в математике.
Рождение гения случилось в 1811 г. в предместье Парижа в семье сторонника Наполеона, вскоре ставшего мэром городка Бур-ля-Рена. До 12 лет мальчик воспитывался матерью, затем поступил в подготовительный Королевский лицей Луи-ле-Гран, законченный когда-то Робеспьером и В.Гюго. Здесь утвердились его либеральные, антироялистские взгляды, переданные от родителей.
Учился юноша неровно: сделав первые успехи, остался на 3 курсе на второй год из-за риторики. Математический гений Галуа пробудил учитель Вернье; ученик, освоив лицейский курс, взялся за труды выдающихся учёных, к примеру, Лагранжа — об алгебраических уравнениях и дифференциальном исчислении. Уйдя с головой в математику, юный гений стал рассеянным и сосредоточенным одновременно, забросил другие науки, чем вызвал негодование учителей – гуманитариев.
Решив поступать в Политехническую школу раньше на год, Галуа провалился из-за краткости решений и недостаточного пояснения. Он знал уже больше преподавателей и недоумевал, почему надо объяснять очевидные вещи.
Поддержка опытного учителя Ришара, его ходатайство о приёме без экзаменов в Политехническую школу благотворно сказались на студенте, его статьи стали появляться в научных журналах. Будучи 17-летним, юноша взялся за решение задачи, почти 300 лет ставившей математиков в тупик: при каких условиях уравнение алгебры можно разрешить? Он искал общий метод, включающий лишь арифметические операции и извлечение корня, то есть разрешение в радикалах.
Кажется, путь его состоял из одних препятствий. В результате клеветы отец Галуа покончил с собой. На вступительном экзамене парень опять провалился – и кинул в экзаменатора тряпкой. Неудачи обостряли его ненависть к консервативным порядкам.
В 1829 г. он стал студентом менее престижной Высшей нормальной школы, из которой спустя год был исключён за то, что назвал директора предателем. Первую статью во Французскую академию наук вундеркинд изложил, ещё учась в лицее. Её рецензент О.Л.Коши предложил представить доработанный труд на конкурс, однако секретарь академии умер, а рукопись исчезла. Конкурс выиграл другой математик. Словно одержимый, Галуа плодотворно работал, публиковал труды в менее академичном издании. Он исследовал условия, определяющие разрешимость уравнений, и сформулировал решение уравнения произвольной степени. В 1831 г. в возрасте 20 лет он представил свой главный труд в Академию.
Краткие работы Галуа были вначале непонятны математикам Гауссу, Якоби, лишь через 15 лет были опубликованы и положили начало теории групп. Его вклад позволил проникнуть в теорию чисел, физику элементарных частиц, кристаллографию, даже создать кубик Рубика.
Студент Галуа был сорвиголовой, регулярно присутствуя на заседаниях академии, нападал на выступающих. Переехав к матери после отчисления из Высшей школы, сын вёл себя так, что мать покинула собственный дом.
Свергнув в 1830 г. короля, республиканцы не смогли установить республику. Галуа участвовал в выступлениях, вступил в Национальную гвардию, вёл себя вызывающе, дважды попадал в тюрьму. О причинах первого заключения рассказал Дюма-отец: на банкете в честь освобождения республиканцев Галуа предложил тост за правящего Луи-Филиппа, «если он предаст», подняв вместе с бокалом кинжал. Второй раз он попал в тюрьму за ношение гвардейской формы (когда опасная гвардия была распущена) на 8 месяцев, оттуда его, заболевшего холерой, перевели в больницу.
Заключение сломило Галуа: уныние сменялось яростью, была попытка самоубийства, его преследовали видения собственной кончины. Он говорил, что погибнет на дуэли, защищая честь кокетки, оскорблённой другим. В частной лечебнице Галуа пережил «бурю страстей», «сладостное блаженство». Источником была дочь врача Стефания дю Мотель, он тяжело переживал прерванные по её инициативе отношения.
В мае 1832 г. Галуа получил смертельное ранение живота на загадочной дуэли, ему не исполнилось ещё 21 года. В ночь перед поединком он отредактировал две рукописи. Даже в тюрьме он продолжал напряжённую мыслительную работу, что говорит о силе интеллекта и воображения. Оригинальнейшая идея математики, требующая холодной головы, родилась в бурное революционное время.
Эварист Галуа обладал многими качествами, которыми наделяют гениев психологи: сосредоточенностью, спонтанностью, сознанием превосходства, вдохновением, воображением. Навязчивые идеи (революции) – тоже характерны для избранных человечества, как и максимализм, экстраординарность. Это не идеал, он не был безупречен, далеко не все окружавшие его люди были глупцами. Но к гению не стоит подходить с обычными мерками, он расширяет границы наших представлений.
Это одна из самых романтичных и трагичных историй жизни учёных: яркая, бескомпромиссная, самоотверженная, поучительная, на полную катушку.
материал с willby.pro
Математики все время норовят описать нашу жизнь как формулу. Порой получается очень убедительно. Но это только до тех пор, пока в игру не вступают чисто человеческие переменные — совесть, доверие, жажда справедливости, эгоизм, альтруизм.
Тут математика перестает работать и начинается как минимум психология.
Мы отобрали десять самых ярких интеллектуальных игр, в основе которых жизнь во всем многообразии ее проявлений.
1. «Ультиматум»: сколько вы готовы заплатить за справедливость?

Правила
Двум игрокам предлагается разделить между собой некоторую сумму денег, допустим 1000 рублей. Первый из них, подающий, предлагает свой вариант дележа, например каждому по 500 рублей, или ему 800, а напарнику — 200 и т. д. Второй игрок, принимающий, может либо согласиться на предложенные условия и получить свою долю, либо отвергнуть схему раздела. Во втором случае никто денег не получает — они уходят обратно в банк.
История и применение
Правила этой игры впервые были сформулированы в 1982 году в Journal of Economic Behaviour and Organization для описания процесса переговоров. Простая в моделировании и парадоксальная в результатах, она быстро стала любимым объектом исследования для ученых всего мира.
Игра «Ультиматум» подходит под многие жизненные ситуации. Например, когда решается вопрос, какую часть прибыли пустить на зарплату сотрудникам, а какую отдать владельцам фирмы.
Человеческие качества
Что бы вы сделали на месте принимающего? Если исходить из рациональности, то надо соглашаться на любой вариант раздела денег. Даже если подающий хочет забрать себе 990 рублей, все равно спорить не стоит: 10 рублей все-таки больше, чем ноль. Но кроме рациональности есть еще и справедливость.
В сотнях проведенных экспериментов подающие чаще всего предлагают своим напарникам от 50 до 30%. Где-то в интервале от 30 до 20% принимающие начинают отказываться от сделки, выбирая принцип «Так не доставайся же ты никому!».
Понимание справедливости зависит от культуры. Перуанские индейцы, к примеру, были склонны принимать практически любые предложения, а жители Азии оказались гораздо щепетильней и несговорчивей американцев. В одном из экспериментов, проведенных в Индонезии, испытуемые отказывались даже от сумм, составляющих несколько их месячных зарплат.
Вообще, психологи немало изгалялись на тему игры «Ультиматум». Оказалось, что на результаты эксперимента влияет множество факторов: сексуальное возбуждение, возраст, степень агрессивности, уровень тестостерона и так далее.
В 2003 году в журнале Science появилась статья об исследовании, в котором работу головного мозга игроков в «Ультиматум» непрерывно отслеживали с помощью МРТ. Оказалось, что у принимающего после получения предложения активизируются островковая доля головного мозга, верхние области лобной коры и поясная извилина. Первая из этих областей считается ответственной за обработку и формирование негативной эмоциональной информации, а другие две — за когнитивные процессы самоконтроля и выбора. Исход этого противостояния древнего механизма эмоций и приобретенного рационального мышления и определяет окончательное решение.
Эксперименты дали неожиданные результаты. Испытуемым искусственно блокировали работу рациональной лобной коры. Казалось бы, отпущенные на свободу эмоции должны в бешенстве отвергать все несправедливые предложения. Но вышло наоборот: игроки стали гораздо более сговорчивыми и податливыми, эмоции гнева и обиды уступили врожденному чувству наживы. Получается, что та самая рациональная деятельность лобной коры и приводит к отклонению от разумной математической стратегии, а представления о чести и справедливости вынуждают людей принимать взвешенно-невыгодное решение. Недаром в экспериментах, проведенных на группах аутистов, процент отказов был значительно ниже. Лишенные социальных предрассудков, они гораздо чаще следовали идеальной математической модели.
2. «Трагедия общинного поля»: если все поступят так
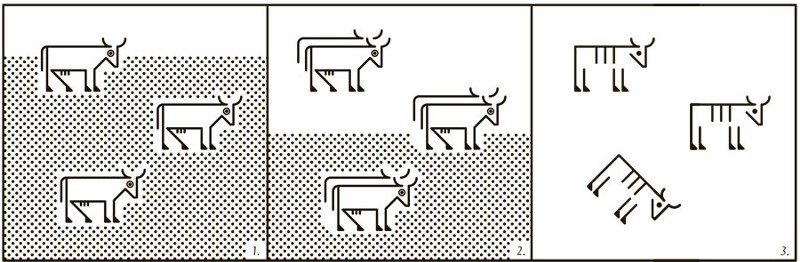
Правила
Жители деревни владеют общим пастбищем. Если каждый будет пасти на нем одну корову, то ничего страшного, травы хватит. Если кто-то захочет завести вторую, то вроде бы тоже все нормально: поле-то большое. Но если каждый станет выпасать по две коровы, то травы на поле не хватит, пастбище истощится, начнется голод.
История и применение
Эту модель предложил Уильям Форстер Ллойд в 1833 году в книге, посвященной перенаселению.
За примерами далеко идти не нужно: в мегаполисах, где пробки стали колоссальной проблемой, а экологическая обстановка ухудшается год от года.
Статьи с различными модификациями этой игры появляются в ведущих научных журналах типа Science и в наше время.
Например, есть вариант эксперимента под названием «Общественное благо». Вот как его описывают ученые из Высшей школы экономики Диляра Валеева и Мария Юдкевич:
«Каждый из участников изначально наделяется определенной суммой денег. Каждый должен частным образом решить, какую долю этих личных денег он может инвестировать в общественное благо. Вложенные в общественное благо деньги увеличиваются в несколько раз и делятся поровну. Группа получит максимальную выгоду, если каждый участник инвестирует всю свою начальную сумму денег. Однако игроки могут уклоняться от вложения своих денег в общественные предприятия. В равновесии, предсказанном теорией, каждый участник вносит нулевой вклад. В реальных экспериментах исход, как правило, иной: игроки вкладывают определенную сумму в общественное благо».
Человеческие качества
Мы не считаем грехом нанести небольшой вред природе или обществу. «От одной брошенной бумажки мир не рухнет» — так рассуждает прохожий, и города зарастают горами мусора.
Социологи и психологи уже давно пытаются понять, как заставить людей быть более альтруистичными. Один из методов — вовлечение человека в процесс, дающее ему ощущение гордости за принесенное благо или сокращение вреда.
Из той же серии распространение музыки через интернет. Некоторые группы предлагают скачать свои произведения бесплатно, а потом, прослушав, заплатить любую сумму. Если не заплатит никто, группе не на что будет записывать новый альбом.
Некоторые экономисты считают, что именно за такими схемами будущее, по крайней мере в области распространения музыки, книг и кино. Например, профессор Высшей школы экономики Александр Долгин вводит понятие «постфактумные благодарственные платежи».
В его схеме экономика будущего сумеет победить халявщиков за счет публичности оценки. Если я прочитал книгу или посмотрел фильм, я должен выставить свою личную оценку — в какой степени мне это понравилось. И будет нелогично, если я поставлю высший балл и при этом не пожертвую автору значительную сумму.
3. «Проблема вагонетки»: можно ли из гуманизма убить человека
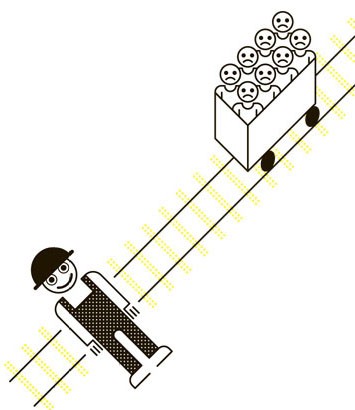
Правила
На железной дороге вот-вот произойдет авария. Вагонетка, наполненная пассажирами, катится в пропасть. У вас есть возможность ее спасти. Для этого надо своими руками столкнуть на рельсы упитанного дорожного рабочего, который случайно оказался рядом. Человек погибнет. Но десятки жизней будут спасены. Вы готовы?
История и применение
Оригинальная формулировка этой мучительной дилеммы была предложена в 1967 году британским философом Филиппой Фут в качестве мысленного эксперимента по этике. За прошедшие годы появилось немало модификаций. Вы убиваете одного и спасаете троих. Вы убиваете ребенка и сохраняете жизнь десятерым. Есть даже пронзительный короткометражный фильм, в котором стрелочник должен выбрать: раздавить собственного сына конструкциями моста или допустить крушение поезда с сотнями пассажиров.
Самое распространенное место применения этой дилеммы, конечно, военные действия. Оставляя взвод прикрывать отступление полка, командир отправляет на верную смерть тридцать человек, но дает шанс тысяче. Но ведь такая ситуация может случиться и на реальной железной дороге. Или во время пожара. Или где-то еще.
Не обязательно речь должна идти о жизни и смерти. Представьте, что вы руководитель отдела, которому нужно уволить одного сотрудника, чтобы сохранить весь коллектив. Или вы ведете урок в школе, и вам приходится накричать на одного ребенка, чтобы весь остальной класс мог спокойно заниматься.
Человеческие качества
В этой игре очень мало математики: десять — это больше, чем один, это даже первоклассник знает. Зато психологии с этикой в этой дилемме навалом. Заповедь «Не убий!» вступает в противоречие с ценностью сохранения жизни. Кстати, в короткометражном фильме про стрелочника главный герой все-таки жертвует своим сыном и поезд с ничего не подозревающими пассажирами преспокойно едет дальше.
В эксперименте, проведенном психологами из Университета Мичигана, испытуемым предлагалась реалистичная трехмерная модель с вагонеткой, путями и необходимостью погубить одного, чтобы спасти пятерых. Около 90% участников переводили стрелку и убивали человека ради пассажиров вагонетки. Но это все-таки компьютерная реальность, а не настоящая жизнь.
4. «Ястребы и голуби»: нападать или бежать

Правила
В одной популяции животных сосуществуют две группы с разными стратегиями борьбы за ресурсы.
- Первые, «ястребы», всегда настроены на конфликт и при встрече с конкурентом идут до конца. В результате они либо выигрывают и присваивают все ресурсы в окрестностях (+50 баллов), либо проигрывают и получают в драке тяжелые увечья (–100 баллов).
- «Голуби», напротив, настроены миролюбиво. Увидев «ястреба», они сразу отступают (0 очков «голубю» и 50 очков «ястребу»), а при встрече со своими сородичами лишь изображают готовность к схватке. После продолжительного обмена угрозами (–10 баллов обоим «голубям») ресурсы достаются более удачливому «голубю» (+50 баллов).
Есть много других вариаций правил, но основные черты игры сохраняются неизменными: победа приносит любой птице среднее количество очков, получение увечий у «ястребов» приравнивается к огромному штрафу, а ритуальные битвы «голубей» тоже требуют некоторых минимальных затрат.
Цель игры предельно проста: заработать максимальное количество очков, что бы за ними ни скрывалось — пища, деньги, самки или «представленность генов индивидуума в генофонде популяции», как выражается Ричард Докинз в своей книге «Эгоистичный ген».
История и применение
Правила игры были впервые опубликованы в журнале Nature в 1973 году. Авторы работы предложили так формализовать конфликты животных за ресурсы, территорию или сексуальных партнеров. Модель позволяет по соотношению стратегий в популяции рассчитать количество ресурсов, затрачиваемых и получаемых особями при том или ином варианте взаимодействий.
Птичью метафору позаимствовали из геополитического сленга того времени («ястребы» — за жесткое противостояние с противником, «голуби» — за разрядку и компромиссы).
«Ястребы и голуби» появились как развитие игры, в которой два водителя несутся навстречу друг другу. Проигравшим считался тот, кто первым испугается лобового столкновения и свернет в сторону.
Человеческие качества
В 2007 году ученые создали виртуальный мир, заселенный агентами, совершающими примитивные действия, которые могли быть скомбинированы в более сложные стратегии. Поведение отдельного агента управлялось собственной нейронной сетью. Это позволило открыть такие стратегии, которые в стандартной теории игр в голову не приходило исследовать.
Так в процессе эволюции этого компьютерного мира в нем появились свои миролюбивые «голуби», «ястребы», нападающие на всех чужаков, и даже «скворцы», собирающиеся в стаи перед лицом опасности. Но самое интересное — что у этих математических агентов стали проявляться возвышенные человеческие чувства: забота о родственниках, самопожертвование и альтруизм.
5. «Пари Паскаля»: бог и выгода
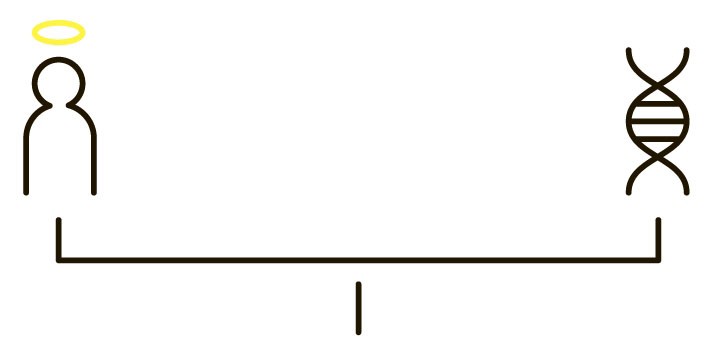
Правила
Каждый из нас в своих отношениях с богом волен выбирать между верой и безверием. В первом случае он несет незначительные расходы на соблюдение ритуалов и подчинение религиозным догмам. Но эти конечные убытки с лихвой окупятся бесконечной прибылью и жизнью вечной, если бог существует. Атеист же, напротив, терпит бесконечные убытки в случае существования бога, зато в жизни повседневной не обременен сакральными расходами.
История и применение
В ночь с 23 на 24 ноября 1654 года на блестящего французского математика и философа, одного из основателей современного математического анализа и теории вероятности Блеза Паскаля снисходит озарение.
Придя в себя, он спешно записывает мысли на кусочек пергамента, который до конца жизни будет носить в подкладке своей одежды. Отныне Паскаль все больше отдаляется от науки и пренебрегает прошлыми забавами — задачками о вероятностях в азартных играх и конструированием машины счета. Делом всей его оставшейся жизни становится так и не оконченный труд «Мысли о религии и других предметах», на страницах которого он и предлагает читателю такое сакральное пари.
В одной из современных медицинских статей проводится параллель между «пари Паскаля» и положением доктора при тяжелобольном пациенте. Врач обязан сделать выбор: сообщить родственникам о возможной скорой смерти больного или дать им надежду: мол, может, все еще обойдется. Говорить о возможности выздоровления психологически менее затратно. Но если больной умрет, для родственников это будет ударом, да и репутация врача пострадает. Признаться в том, что пациент, скорее всего, умрет, сложнее. Но если вдруг больной выздоровеет, врачу угрожает лишь слава циничного гения. Авторы статьи рекомендуют врачам придерживаться нелегкой роли пессимиста.
Человеческие качества
«Пари Паскаля» подчеркивает парадоксальное желание человека объяснить иррациональную веру с позиций разума и математической выгоды. Десятки мыслителей позднее указывали на слабости этой аргументации. Пари противоречит и религиозным канонам. Ведь вера «на всякий случай», формальное отправление ритуалов в ущерб внутреннему содержанию может оказаться большим грехом, чем атеизм.
6. «Парадокс блондинки»: как нобелевский лауреат Джон Нэш учил ухаживать за девушками
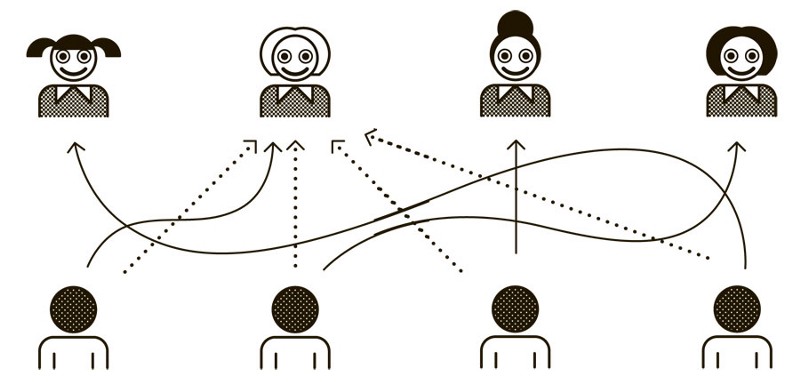
Правила
Компания неженатых молодых людей проводит вечер в баре. Они замечают за соседним столиком компанию девушек — прекрасную блондинку и несколько менее симпатичных брюнеток и шатенок. Как начать за ними ухаживать?
История и применение
«Если мы все рванем к блондинке, то помешаем друг другу и она не достанется никому. Тогда мы займемся подружками, и они оттолкнут нас — никто не хочет быть вторым сортом. А вот если ее никто не заметит, мы не будем толкаться и не оскорбим других девушек. Так мы выиграем. Лишь так получим женщин. Адам Смит считал, что лучше всего, когда каждый член группы действует в своих интересах. Это правда, но не вся. На деле результат будет оптимальным, если каждый член группы сделает как лучше для себя и для группы» — это цитата из фильма «Игры разума».
Прототипом главного героя стал математик, нобелевский лауреат Джон Нэш, знаменитый тем, что сумел побороть симптомы шизофрении.
Неизвестно, была ли ситуация с блондинкой реальной. Но премию имени Нобеля Джон Нэш получил как раз за разработку теории игр. До него математики занимались в основном играми «с нулевой суммой» — это когда выигрыш равен проигрышу, блондинка достается либо одному, либо другому. Нэш занимался теми ситуациями, когда сумма не равна нулю, то есть кому-то достается брюнетка, кому-то — шатенка.
Нобелевку он получил за стратегию игры, которая сейчас называется «равновесие по Нэшу». Энциклопедии описывают ее так: «Ситуация, в которой ни один участник не может увеличить выигрыш, изменив свое решение в одностороннем порядке, когда другие участники не меняют решения».
Понятное дело, что при знакомстве с барышнями в баре мало кто использует математику (если только вы не будущий нобелевский лауреат). Зато эти формулы очень хорошо работают в бизнесе — собственно, премия досталась Нэшу именно в номинации «Экономика».
Человеческие качества
Бытовая мораль из трудов гениального математика очень проста: сотрудничать лучше, чем конкурировать.
7. «Дуэль на троих»: побеждает слабейший
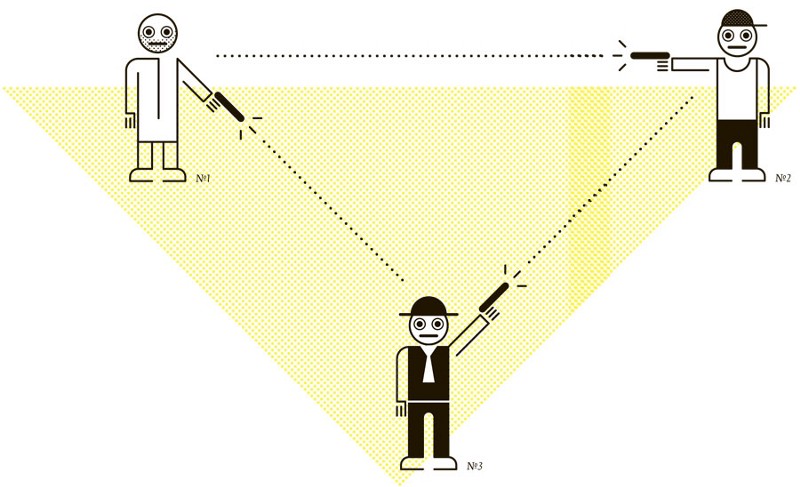
Правила
Три человека стоят в вершинах правильного треугольника и поочередно стреляют друг в друга. Победившим считается тот, кто выжил.
История и применение
Первый раз такой сценарий появился в статье американского математика Киннарда в 1946 году.
После появились многочисленные модификации правил: увеличивалось количество игроков, изменялось их мастерство, вводились одновременные выстрелы или даже пацифистские залпы в воздух.
Во всех вариациях наблюдается одна тенденция: чем слабее стрелок, тем выше его шансы на победу. Ведь логичнее уничтожить сначала самого сильного соперника. Этот парадокс можно порой наблюдать на рынке. Ведущие корпорации сражаются друг с другом, наносят маркетинговые удары. В результате вперед вырывается какая-нибудь второстепенная фирма, с которой просто никто не боролся. Аналогичную картину можно наблюдать в любом соревновании, будь то спорт, выборы или борьба за должность.
Человеческие качества
Здесь математика оказывается на службе справедливости. Сильные так увлечены борьбой друг с другом, что слабые наконец получают свой шанс.
8. «Аукцион»: продать 20 долларов за 204
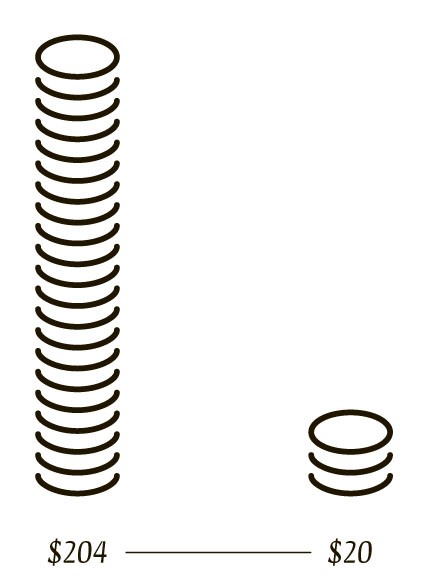
Правила
На торги выставлена купюра в двадцать долларов. Участники предлагают свою цену, начиная от 1 доллара. Купюра достается тому, кто предложит самую высокую ставку. Владельцу двадцатки достается и сумма той ставки, которая предлагалась перед финальной.
История и применение
Эту игру из года в год проводит со своими студентами Макс Базерман, профессор Гарвардской школы бизнеса. Он показывает аудитории двадцатидолларовую купюру и обещает продать ее человеку, ставка которого окажется максимальной. Теоретически какой-нибудь счастливчик вполне может приобрести двадцатку за 15 долларов. Профессор вдобавок к этим 15 получает еще и 14 от того бедолаги, чья ставка оказалась предшествующей.
Рекорд Бразермана — 204 доллара. Поначалу студенты с радостью принимают возможность нажиться на чудаковатом лекторе и энергично повышают ставки, но уже с 15 долларов большинство из них понемногу выходят из игры. Подмечено, что тогда же меняется и поведение игроков: на смену рациональным ставкам в духе «ситуация под контролем» приходят нервные, рискованные и неадекватные ходы. После превышения номинальных 20 долларов в игре обычно остается только пара неудачников, которые дальше отчаянно пытаются свести свои расходы к минимуму и неуклонно поднимают ставку в страхе оказаться предпоследним.
Естественно, игра проводится не ради прибыли Базермана (профессора в Гарварде и так неплохо зарабатывают). Борьба за двадцатку раскрывает механизм работы аукционов, азартных игр и прочих систем, в которых возникает дилемма: зафиксировать убытки или попытаться отыграться.
Человеческие качества
Жадность, ум и глупость, расчетливость, азартность, гордость, настойчивость, недальновидность.
9. «Марьяж»: Нобелевка за правильную организацию женитьбы

Правила
Даны два множества элементов — мужчины и женщины. Для каждого из них существует определенная система приоритетов в выборе партнера. Требуется разбить этих привередливых людей на идеально устойчивые пары: ни один из супругов не должен испытывать взаимного притяжения к чужому партнеру (неразделенные страсти никто не запрещает). В разных вариантах правил меняются выбирающая сторона (матриархат/патриархат), количество мужчин и женщин или разрешается многоженство.
История
Статья «Поступление в колледж и стабильность браков» Дэвида Гейла и Ллойда Шепли появилась в научном журнале American Mathematical Monthly в 1962 году. А в 2012-м Шепли получил за эту работу Нобелевскую премию по экономике.
Для решения задачи они предложили следующий патриархальный алгоритм. Сначала каждый жених идет с предложением руки и сердца к номеру один своего списка. Дальше женщины отвечают самым понравившимся кандидатам расплывчатым «может быть», а остальных отправляют восвояси.
После этого неудачливые женихи стучатся в дверь своих вице-фавориток, и девушки вновь раздают желанные «может быть» (если новый жених понравился больше предыдущего, они даже могут разорвать «помолвку» первого этапа). Этот сценарий повторяется до тех пор, пока все женихи не смогут добиться целомудренного согласия невест, которое в конце игры магическим образом превращается в твердое «согласна».
Неизвестно, пытался ли кто-то именно так искать себе жену в реальности. Зато разработанный в статье алгоритм с успехом использовался для распределения студентов по колледжам, докторов по клиникам и даже донорских органов по больным. За это, собственно, и дали премию имени Нобеля.
Человеческие качества
Кажется, в этом несложном алгоритме можно вечно находить все новые детали. Так, игра заканчивается на первом же раунде, если всем мужчинам нравятся разные женщины. Феминистки тут должны возмутиться, ведь в этом случае мнение невест вообще не учитывается.
К тому же стабильность разбиения еще совсем не означает всеобщего счастья: многие мужчины и женщины могут мечтать о чужих супругах, главное — чтоб без взаимности,
10. «Дилемма заключенного»: стучать или молчать?
Правила
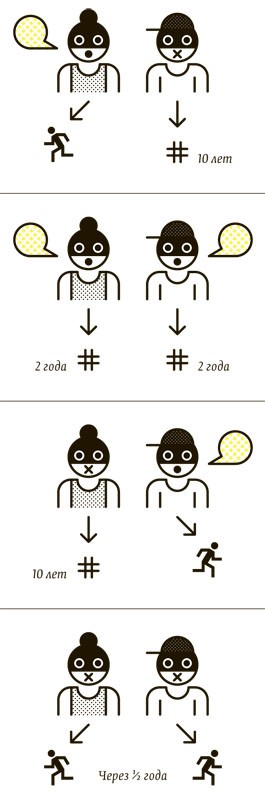
Представьте, что вы попытались ограбить банк. Но, увы, вас и вашего подельника поймали и рассадили по разным камерам.
Следователь предлагает сделку: вы даете показания против своего напарника и тогда получаете шанс на освобождение за помощь следствию.
У вас есть четыре варианта действий:
1. Вы соглашаетесь и даете показания. Ваш напарник молчит. Тогда он получает десять лет, а вы выходите на свободу.
2. Вы колетесь, и ваш напарник колется. Тогда вы оба получаете по два года.
3. Вы гордо молчите, но ваш подельник дает показания. Тогда на свободу выходит он, а вы получаете десять лет.
4. Вы оба молчите, и через шесть месяцев вас отпускают за недостатком доказательств.
И что вы выбираете? Следователь уже открывает дверь вашей камеры…
История и применение
Базовую модель «Дилеммы заключенного» предложили в 1950 году американские математики Меррил Флад и Мелвин Дрешер, работавшие на исследовательскую корпорацию RAND. Эта игра была нужна для прогнозирования гонки ядерных вооружений — в роли заключенных выступали СССР и США.
С тех пор игра стала очень популярна среди математиков, философов и психологов. Уходя с военно-криминальной обложки, можно обнаружить и много других примеров. Ту же гонку вооружений сейчас очень напоминают рекламные кампании. Постоянное соревнование в количестве рекламного контента неуклонно увеличивает расходы фирм. Соответственно, от прекращения гонки выиграли бы все стороны. Но если кто-то вероломно нарушит перемирие, он выиграет войну за потребителя, а остальные проиграют.
В США даже проводились соревнования между командами университетов на лучшую запрограммированную стратегию игры в «Дилемму заключенного», где победа присуждалась за минимальный срок заключения по итогам нескольких раундов допросов. Победила программа, основанная на принципе «око за око»: она поступала с каждым своим напарником в точности так, как с ней поступили ходом ранее. Но это все-таки математика, человеческая жизнь куда сложнее.
Человеческие качества
Основная проблема «Дилеммы заключенного» — доверие. Именно из-за нежелания доверять другому и возникает конфликт интересов, который возвели в абсолют, к примеру, сценаристы серии хорроров «Пила». Так, в пятой части герои могут отделаться в прямом смысле малой кровью, чтобы выбраться из ловушки. Но вместо этого они начинают соперничать, что приводит к гибели большинства из них.
Источник: expert.ru

Что это такое, и с чем его едят.
Теория игр — это раздел математической экономики, изучающий решение конфликтов между игроками и оптимальность их стратегий. Конфликт может относиться к разным областям человеческого интереса: чаще всего это экономика, социология, политология, реже биология, кибернетика и даже военное дело. Конфликтом является любая ситуация, в которой затронуты интересу двух и более участников, традиционно называемых игроками. Для каждого игрока существует определенный набор стратегий, которые он может применить. Пересекаясь, стратегии нескольких игроков создают определенную ситуацию, в которой каждый игрок получает определенный результат, называемый выигрышем, положительным или отрицательным. При выборе стратегии важно учитывать не только получение максимального профита для себя, но так же возможные шаги противника, и их влияние на ситуацию в целом.
Краткая история развития.

Основы теории игр зародились еще в 18 веке, с началом эпохи просвящения и развитием экономической теории. Впервые математические аспекты и приложения теории были изложены в классической книге 1944 года Джона фон Неймана и Оскара Моргенштерна «Теория игр и экономическое поведение». Первые концепции теории игр анализировали антагонистические игры, когда есть проигравшие и выигравшие за их счет игроки. Не смотря на то, что теория игр рассматривала экономические модели, вплоть до 50-х годов 20 века она была всего лишь математической теорией. После, в результате резкого скачка экономики США после второй мировой войны, и, как следствие, большего финансирования науки, начинаются попытки практического применения теории игр в экономике, биологии, кибернетике, технике, антропологии. Во время Второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней мощный аппарат для исследования стратегических решений. В начале 50-х Джон Нэш (на фото) разрабатывает методы анализа, в которых все участники или выигрывают, или терпят поражение. Эти ситуации получили названия «равновесие по Нэшу». По его теории, стороны должны использовать оптимальную стратегию, что приводит к созданию устойчивого равновесия. Игрокам выгодно сохранять это равновесие, так как любое изменение ухудшит их положение. Эти работы Нэша сделали серьезный вклад в развитие теории игр, были пересмотрены математические инструменты экономического моделирования. Джон Нэш показывает, что классический подход к конкуренции А.Смита, когда каждый сам за себя, неоптимален. Более оптимальны стратегии, когда каждый старается сделать лучше для себя, делая лучше для других. За последние 20 — 30 лет значение теории игр и интерес значительно растет, некоторые направления современной экономической теории невозможно изложить без применения теории игр.Большим вкладом в применение теории игр стала работа Томаса Шеллинга, нобелевского лауреата по экономике 2005 г. «Стратегия конфликта».
Как это работает
Как мне кажется, смысл теории игр проще всего пояснить на «Дилемме заключенного», классическая формулировка которой звучит так:
Двое преступников, А и Б, попались примерно в одно и то же время на сходных преступлениях. Есть основания полагать, что они действовали по сговору, и полиция, изолировав их друг от друга, предлагает им одну и ту же сделку: если один свидетельствует против другого, а тот хранит молчание, то первый освобождается за помощь следствию, а второй получает максимальный срок лишения свободы (10 лет). Если оба молчат, их деяние проходит по более лёгкой статье, и они приговариваются к 6 месяцам. Если оба свидетельствуют против друг друга, они получают минимальный срок (по 2 года). Каждый заключённый выбирает, молчать или свидетельствовать против другого. Однако ни один из них не знает точно, что сделает другой. Что произойдёт?
Представив игру в виде матрицы мы получим:
| Преступник Б Стратегия «молчать» |
Преступник Б Стратегия «предать» |
|
|---|---|---|
| Преступник А Стратегия «молчать» |
Пол года каждому | 10 Лет преступнику А Отпустить преступника Б |
| Преступник А Стратегия «предать» |
10 Лет преступнику Б Отпустить преступника А |
2 года каждому |
А теперь представим развитие ситуации, поставив себя на место заключенного А. Если мой подельник молчит, лучше его сдать и выйти на свободу. Если он говорит, то так же лучше все рассказать, и получить всего два года, вместо десяти. Таким образом, если каждый игрок выбирает, что лучше для него, оба сдадут друг друга, и получат два года, что не является идеальной ситуацией для обоих. Если бы каждый думал об общем благе, они бы получили всего по пол года.
Типы игр
Кооперативная\некооперативная игра
Кооперативной игрой является конфликт, в котором игроки могут общаться между собой и объединяться в группы для достижения наилучшего результата. Примером кооперативной игры можно считать карточную игру Бридж, где очки каждого игрока считаются индивидуально, но выигрывает пара, набравшая наибольшую сумму. Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом. Не смотря на то, что эти два вида противоположны друг другу, вполне возможно объединение стратегий, которое может принести больше пользы, чем следование какой-либо одной.
С нулевой суммой и с ненулевой суммой
Игрой с нулевой суммой называют игру, в которой выигрыш одного игрока равняется проигрышу другого. Например банальный спор: если вы выиграли сумму N, то кто-то эту же сумму N проиграл. В игре же с ненулевой суммой может изменяться общая цена игры, таким образом принося выгоду одному игроку, не отнимаю ее цену у другого. В качестве примера здесь отлично подойдут шахматы: превращая пешку в ферзя игрок А увеличивает общую сумму своих фигур, при этом не отнимая ничего у игрока Б. В играх с ненулевой суммой проигрыш одного из игроков не является обязательным условием, хотя такой исход и не исключается.
Параллельные и последовательные
Параллельной является игра, в которой игроки делают ходы одновременно, либо ход одного игрока неизвестен другому, пока не завершится общий цикл. В последовательной игре каждый игрок владеет информацией о предидущем ходе своего оппонента до того, как сделать свой выбор. И совсем не обязательно информации быть полной, что подводит на с кледующему типу.
С полной или неполной информацией
Эти типы являются подвидом последовательных игр, и названия их говорят сами за себя.
Метаигры
Эти игры являются «леммами» теории игр. Они полезны не сами по себе, а в контексте какого-либо конфликата, расширяя его набор правил.
В любом конфликте типы объединяются, определяя таким образом правила игры, будь это кооперативная последовательная игра с нулевой суммой, или метаигра с неполной информацией.
Проблемы практического применения
Безусловно, следует указать и на наличие определенных границ применения аналитического инструментария теории игр. В следующих случаях он может быть использован лишь при условии получения дополнительной информации.
Во-первых, это тот случай, когда у игроков сложились разные представления об игре, в которой они участвуют, или когда они недостаточно информированы о возможностях друг друга. Например, может иметь место неясная информация о платежах конкурента (структуре издержек). Если неполнотой характеризуется не слишком сложная информация, то можно применять опыт подобных случаев с учетом определенных различий.
Во-вторых, теорию игр трудно применять при множестве ситуаций равновесия. Эта проблема может возникнуть даже в ходе простых игр с одновременным выбором стратегических решений.
В-третьих, если ситуация принятия стратегических решений очень сложна, то игроки часто не могут выбрать лучшие для себя варианты. Например, на рынок в разные сроки могут вступить несколько предприятий или реакция уже действующих там предприятий может оказаться более сложной, нежели быть агрессивной или дружественной.
Экспериментально доказано, что при расширении игры до десяти и более этапов игроки уже не в состоянии пользоваться соответствующими алгоритмами и продолжать игру с равновесными стратегиями.
К сожалению, ситуации реального мира зачастую очень сложны и настолько быстро изменяются, что невозможно точно спрогнозировать, как отреагируют конкуренты на изменение тактики. Тем не менее, теория игр полезна, когда требуется определить наиболее важные и требующие учета факторы в ситуации принятия решений в условиях конкурентной борьбы. Эта информация важна, поскольку позволяет учесть дополнительные переменные или факторы, имеющие возможность повлиять на ситуацию, и тем самым повысить эффективность решения.
Заключение
В заключение следует особо подчеркнуть, что теория игр является очень сложной областью знания. При обращении к ней надо соблюдать известную осторожность и четко знать границы применения. Слишком простые толкования таят в себе скрытую опасность. Анализ и консультации на основе теории игр из-за их сложности рекомендуются лишь для особо важных проблемных областей. Опыт показывает, что использование соответствующего инструментария предпочтительно при принятии однократных, принципиально важных плановых стратегических решений, в том числе при подготовке крупных кооперационных договоров.
Если тема окажется интересной для сообщества, следующих статьях я попытаюсь подробнее раскрыть типы игр и их стратегии.
Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.
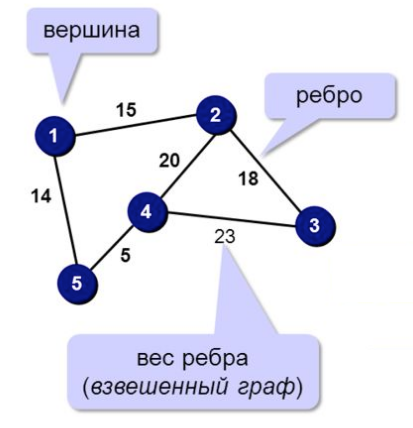
Теория графов находит применение, например, в геоинформационных системах. Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра.
Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.
История возникновения теории графов
Родоначальником теории графов считается выдающийся математик, член Петербургской академии наук Леонард Эйлер.
В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.
В 1736 году задача о семи мостах заинтересовала Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя».
На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:
- Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
- Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
- Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Изображение графов на плоскости
При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов).

Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются отрезком или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра.
Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление.
Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.
Социальный граф
Социальный граф (англ. Social graph) — это граф, узлы которого представлены социальными объектами, такими как пользовательские профили с различными атрибутами (например: имя, день рождения, родной город и т. д.), сообщества, медиа-контент и т. д., а ребра — социальными связями между ними.

Неявный социальный граф (англ. Implicit social graph) — это такой граф, который можно сформировать на основе взаимодействий пользователя со своими «друзьями» и группами «друзей» в социальной сети. В этом графе в отличие от обычного социального графа нет явного указания «друзей», то есть нет явных социальных связей.
С помощью социальных графов решают такие задачи, как: идентификация пользователей; социальный поиск; генерация рекомендаций по выбору «друзей», медиа-контента, новостей; выявление «реальных» связей или сбор открытой информации для моделирования графа.
Обработка данных социальных графов связана с рядом проблем, как например различия социальных сетей, закрытость социальных данных.
Задачи
Идентификация пользователей
Обнаружение профилей, принадлежащих одному человеку, в нескольких социальных сетях. Решение этой задачи позволяет получить более полный социальный граф, что может быть полезно во многих задачах, таких как:
Социальный поиск
Поиск социальных объектов (пользователей, их данных, их записей и т. д.), основанный на анализе набора связей, в которых находятся искомые объекты.
Генерация рекомендаций
Важной задачей является поиск точных алгоритмов генерации рекомендаций и предложений пользователям, который так же используется при создании графа интересов на основе социального графа.
- Рекомендация друзей — пользователи редко делят свои контакты на социальные группы, но, тем не менее, они неявно делят эти контакты на кластеры, через их взаимодействия в рамках социальной сети.
- Рекомендации контента — рекомендации медиа-контента, сообществ, новостей и т. п.
Существуют традиционные подходы в области рекомендательных систем:
- Коллаборативная фильтрация — заключается в формировании списка рекомендованных объектов на основе мнений пользователей, ведущих себя похожим образом.
- Фильтрация содержимого — основывается на характеристиках предмета и известной о нем информации.
- Социальные подходы — отталкиваются от социальных связей пользователей.
Выявление «настоящих» связей
Применение подхода «разведки на основе открытых источников» для выявления истинных связей между пользователями, то есть настоящих друзей, родственников и т. п.
Граф интересов
Граф интересов — это онлайн представление интересов конкретного человека, полученное на основе его активности в социальных сетях.

Вершинами графа являются увлечения личности, также вершиной может быть профиль человека в социальной сети, ребра графа отображают взаимоотношения между вершинами графа.
С помощью графа интересов можно понять, что человек хочет сделать, купить, куда хочет пойти, с кем может встретиться, за чьими сообщениями ему интересно следить или за кого он готов проголосовать.
Cвязи в графе интересов
В графе интересов могут существовать различные типы связей, которые позволяют пользователю выходить за рамки обычных социальных сетей. Например, человеку нужно найти ответ на интересующую его тему, который не может дать ни один из старых друзей и знакомых. В этом случае выстраивается цепочка из трех типов связей:
- человек-человек (пользователи в социальной сети могут взаимодействовать напрямую)
- человек-интерес (то с чем пользователь взаимодействует с социальной сети)
- интерес-интерес (схожие интересы могут быть взаимосвязаны)
Граф интересов также может быть представлен в виде взвешенного графа, в этом случае вес ребра означает силу взаимосвязи между вершинами.
При построении такого графа изначально вводится предположение о том, что взаимосвязи имеют одинаковую силу, например, интерес к машинам и к театру неизвестен, и взаимосвязь двух интересов устанавливается в виде бесконечно большого числа. Затем, если будет обнаружено, что люди, интересующиеся машинами, ведут себя похожим образом с теми людьми, которые увлекаются театром, то значение веса ребра между вершинами, обозначающими данные увлечения, будет уменьшено.
Отношения между графом интересов и социальным графом
Граф интересов и социальный граф тесно взаимосвязаны, но это не одно и то же.
Граф интересов используется для создания сети интересов людей. В то время как Facebook и другие социальные сети организованы вокруг друзей человека, то есть вокруг социального графа, сети увлечений созданы вокруг интересов личностей, их графа интересов.
Подобно тому как социальный граф — это карта взаимосвязей личности с теми, кто «следует» за ней в сети, граф интересов — это так же взаимосвязь с интересами личности в сети.
Таким образом, увлечения человека, представленные в виде графа интересов, обеспечивают средства для дальнейшей персонализации веб-пространства, основанной на пересечении графа интересов с веб-контентом. Граф интересов или сеть интересов в некоторых случаях могут быть получены из социального графа или социальной сети и могут поддерживать и обновлять связи между вершинами на основе данной социальной сети.
Граф интересов должен быть точным и выразительным, он должен принимать во внимание явно объявленные интересы, например, «Like» на Facebook или «интересы» в профиле на LinkedIn, а также неявные интересы, выведенные на основе активности пользователя, например, такие как щелчки мышью, комментарии, теги к фото и чек-ины. Социальные сети часто являются источником этой информации.
Использование графа интересов
Существует несколько способов использования графа интересов, как с точки зрения потребителя, так и с точки зрения бизнесмена. В сочетании с социальным графом, граф интересов может быть применён для установления связей между пользователями в социальных сетях или в реальном мире. В таких сетях пользователи могут указывать и делиться своими увлечениями, но при этом им не обязательно знать друг друга.
Граф интересов так же может быть применён в маркетинге, в целях анализа аудитории проекта и дальнейших продаж на основе этой информации, для анализа тональности текста и для таргетированной рекламы, основанной на интересах.
Например, такие компании как Twitter с помощью графа интересов имеют возможность делать рекламу более направленной на конкретного пользователя, основываясь на его увлечениях.
Также граф интересов может использоваться при создании продукции с учётом пожеланий потребителя, он помогает определить какие особенности и возможности следует предоставить в следующих версиях. Граф интересов имеет множество других применений включая задачи обнаружения содержимого и фильтрации для предоставления рекомендаций по фильмам, книгам, музыке и так далее.
материал с medium.com
Одна из величайших загадок математики − существует ли упорядоченная структура в распределении простых чисел? Ученые с помощью генерации числовых сетей пытаются определить связи между простыми и составными числами, надеясь пролить свет на эту тайну.

Загадка распределения простых чисел
©wallpaperno.com
Простыми, как известно, называются целые положительные (натуральные) числа, которые имеют лишь два натуральных делителя: единицу и само число. Фактически они являются строительными блоками для всех составных чисел − произведений простых.
Список первых простых чисел − до 300:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293
Распределение простых чисел среди множества натуральных всегда вызывало огромный интерес среди математиков. Многие полагали, что в нем кроется некая скрытая логика, своеобразный узор.
Мариан Богунья и ее коллеги из Барселонского университета решили разгадать тайну распределения простых чисел с помощью сетей.
Они создали компьютерную программу, которая произвела сетевую структуру, связавшую простые числа от 2 до миллиарда со всеми их произведениями − составными числами.
Им также удалось разработать серию схожих числовых сетей, используя простые правила объединения чисел. Математиков интересовало, смогут ли они таким образом нащупать структуру, похожую на распределение простых чисел среди всех натуральных.
Правила построения числовых структур менялись по вероятностным законам, поэтому полученные сети оказывались каждый раз разными. Исследователи обнаружили, что сгенерированные сети были действительно очень схожи с реальной системой связей простых и составных чисел.
В своей предыдущей работе исследователям удалось найти способ приблизительной оценки количества простых чисел до определенного граничного значения. В дальнейшем группа Марион Богунья рассчитывает еще больше приблизиться к сетевой структуре простых чисел, применяя новые правила построения сетей.
До сих пор проверка различных теорий о простых числах наталкивалась на большие трудности, поскольку не существовало методик построения подобных структур.
Ученые рассчитывают, что продолжение их исследований поможет также пролить свет на знаменитую гипотезу Римана:
Все нетривиальные нули дзета-функции имеют действительную часть, равную 1/2.
Гипотеза Римана входит в список семи «проблем тысячелетия», за решение каждой из которых Математический институт Клэя выплатит награду в один миллион американских долларов.
материал с naked-science.ru



