математика













В свое время, когда я только начинал работать репетитором я столкнулся с ситуаций, что для многих школьников решение квадратного уравнения является большой проблемой. Поэтому давайте попробуем вместе сделать все поэтапно.
1) Для начала выясним — что же такое квадратное уравнение?
Квадратное уравнение — это уравнение вида ax^2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Вот например:
х^2 + 3х — 4 = 0
Здесь a = 1; b = 3; c = -4 (обратите внимание — минус — тоже записываем)
2) Квадратные уравнения делятся на три типа — те которые имеют два вещественных корня, те которые имеют один вещественный корень и те, которые не имеют вещественных корней.
Определить к какому типо относится уравнение нам помогает дискриминант. Обозначается он буквой D и находится он таким образом:
D = b^2 − 4ac
В зависимости от значения дискриминанта можно определить сколько корней имеет наше квадратное уравнение:
Если D < 0, корней нет;
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.
Вот например:
x^2 − 8x + 12 = 0;
a = 1; b = -8; c = 12;
D = (-8)^2-4*1*12 = 64 — 48 = 16 > 0 => уравнение имеет два корня
3) И последний этап: находим, собственно корни
Если дискриминант D > 0, корни можно найти по формулам:
х1 = (- b + √D)/2a;
x2 = (- b — √D)/2a;
Когда D = 0, то
х = — b/2a;
И если D < 0, корней нет — ничего считать не надо.
Вот например:
-x^2 — 2x +15 = 0;
a = -1; b = -2; c = 15;
D = (-2)^2 — 4*(-1)*15 = 64 > 0
У уравнения есть два корня.
х1 = (- (-2) + √64)/(2*(-1)) = (2 + 8) / -2 = -5;
х2 = (- (-2) — √64)/(2*(-1)) = (2 — 8) / -2 = 3;
Это и есть корни нашего уравнения: -5 и 3.
И в заключении хотелось бы привести мнемоническое правило для запоминания формулы корней квадратного уравнения подсказанное несравненной участницей нашей группы Мариной Комаровой:
Не побьёт теперь никто лень,
В голове у всех дыра:
Минус «бэ» плюс-минус корень
Разделить на дважды «а».
А под корнем — мыслим шире
С хитрой миной на лице —
«Бэ» квадрат отнять четыре
«А» умноженных на «цэ»
Сегодня тема нашего урока опять тригонометрия, но сегодня для запоминания ненавистных нам синусов и косинусов будем использовать мнемонику.
Что ж такое мнемоника, спросите Вы? Так вот, мнемоника — это такой способ запоминания какой-либо информации, когда вы сложные для вас понятия представляете в виде каких-либо наглядных образов.
Например:
1) Производные синуса и косинуса находятся по формулам: (sin a)’ = cos a и (cos a)’ = -sin a. Всё очень просто: нужно синус заменить на косинус, косинус на синус и не запутаться со знаком. Эти формулы можно записать в следующем виде:
Синий косяк.
Косяк – синий.
Зная правила правописания вопрос со знаком решается сам собой.
2) Кстати: для определения синуса и косинуса также существует запоминалка.
Синус и косинус угла задаётся на основе соотношений в прямоугольном треугольнике.
Синус угла определяется как отношение противолежащего, к данному углу, катета к гипотенузе
Косинус это как отношение прилежащего катета к гипотенузе.
Чтобы не запутаться что используется с чем можно использовать следующую ассоциацию:
Косинус – косяк – дверь – дверь приложена (прилежащий катет) к косяку. Т.е. Косинус угла это отношение прилежащего катета к гипотенузе. Ну а противолежащий достаётся синусу.
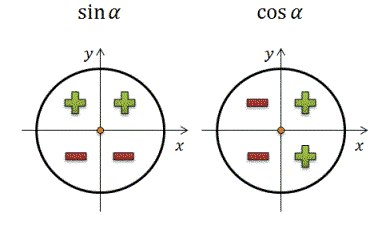
3) Для нахождения значений и знака синуса на единичной окружности используется ордината или ось Y, косинуса – абсцисса или ось X. Для их запоминания используется следующая запоминалка:
Синус — синий – синее небо. На синее небо, вверх, указывает ось Y. Значит ось X достаётся косинусу. (см. рисунок)

Сегодня тема нашего урока опять тригонометрия, но сегодня для запоминания ненавистных нам синусов и косинусов будем использовать мнемонику.
Что ж такое мнемоника, спросите Вы? Так вот, мнемоника — это такой способ запоминания какой-либо информации, когда вы сложные для вас понятия представляете в виде каких-либо наглядных образов.
Например:
1) Производные синуса и косинуса находятся по формулам: (sin a)’ = cos a и (cos a)’ = -sin a. Всё очень просто: нужно синус заменить на косинус, косинус на синус и не запутаться со знаком. Эти формулы можно записать в следующем виде:
Синий косяк.
Косяк – синий.
Зная правила правописания вопрос со знаком решается сам собой.
2) Кстати: для определения синуса и косинуса также существует запоминалка.
Синус и косинус угла задаётся на основе соотношений в прямоугольном треугольнике.
Синус угла определяется как отношение противолежащего, к данному углу, катета к гипотенузе
Косинус это как отношение прилежащего катета к гипотенузе.
Чтобы не запутаться что используется с чем можно использовать следующую ассоциацию:
Косинус – косяк – дверь – дверь приложена (прилежащий катет) к косяку. Т.е. Косинус угла это отношение прилежащего катета к гипотенузе. Ну а противолежащий достаётся синусу.
3) Для нахождения значений и знака синуса на единичной окружности используется ордината или ось Y, косинуса – абсцисса или ось X. Для их запоминания используется следующая запоминалка:
Синус — синий – синее небо. На синее небо, вверх, указывает ось Y. Значит ось X достаётся косинусу. (см. рисунок)

Фокусы — это всегда хорошо. Особенно математические. Они могут не только развлечь компанию, но и создать у зрителей впечатление, что они столкнулись с самим Перельманом или Эйнтштейном.
1
ДЕНЬ РОЖДЕНИЯ

Предположим, Вам вдруг понадобилось поразить собеседника (цу) своими комбинаторными способностями, а испещренную расчетами доску Вы оставили дома. Есть способ — угадайте день рождения человека без калькулятора и заглядывания на его страницу в социальной сети.
Предложите собеседнику (це) умножить дату дня рождения на три. После чего попросите поделить полученное число на девять. Не всякое число делится на девять без остатка, поэтому, скорее всего, полученное число будет состоять из частного и остатка. Донесите эту простую, но нужную сентенцию до собеседника (цы). Пусть он (она) умножит частное на три, а остаток на три поделит. После чего просто сложит полученные числа. Всё. Вы можете назвать число.
Для наглядности. Предположим, Вы родились 8 числа.
1) 8*3=24
2) 24:9=2 (6)
3) 2*3=6
4) 6:3=2
5) 6+2= 8
2
СКОЛЬКО ЛЕТ?

Этот математический фокус лучше показывать мужчинам. Возраст — дело деликатное. Итак, предложите товарищу умножить его возраст на пять. Пусть к полученной сумме он прибавит восемь, а результат умножит на два. Из этого числа нужно вычесть шесть, а полученную сумму умножить на 10. Из результата Вы вычитаете 100 и на 100 же делите. Перед Вами — возраст собеседника.
Для наглядности. Предположим, Вам 20 лет.
1) 20*5=100
2) 100+8+108
3) 108*2=216
4) 216-6=210
5) 210*10=2100
6) 2100-100=2000
7) 2000:100=20
3
ДВУЗНАЧНОЕ ЧИСЛО

Отгадывание чисел интересно тем, что человек, которому Вы предлагаете поучаствовать в математическом аттракционе будет стараться загадать число «послсожнее», хотя математика таких понятий не знает. Есть алгоритм — он Вам и поможет в «магии».
Пусть Ваш товарищ загадает любое двузначное число. Потом разделит его на три, на пять и на семь, а остатки от каждого деления назовет Вам. Вы с легкостью отгадаете число. Как? Сейчас объясним.
Остаток деления на три умножаете на семьдесят, остаток деления на пять умножаете на двадцать один, а остаток деления на семь умножаете на пятнадцать. Полученные числа нужно сложить и поделить на 105. Всё. Полученный при делении остаток — возраст.
Для наглядности. Предположим, задуманное число 25.
1) 25:3=8 (1)
2) 25:5=5 (0)
3) 25:7=3 (4)
4) 1*70=70
5) 0*21=0
6) 4*15=60
7) 60+70=130
8) 130:105=1(25)
4
ФОКУС СО СЛОЖЕНИЕМ МНОГОЗНАЧНЫХ ЧИСЕЛ

Сложение чисел — одна из простейших операций, особенно, если числа однозначные. Но когда нужно складывать многозначные числа — дело усложняется. Только не для Вас, ведь Вы знаете математическую «магию».
Итак, попросите того, с кем Вы решили посоревноваться в скорости счета, написать несколько чисел с одинаковым количеством знаков. Чем больше — тем лучше. Потом припишите к этому длинному ряду чисел свои. Затем предложите сложить все числа на скорость. Чтобы победить в этом соревновании — нужно знать секрет.
Вот он: написанные Вами числа должны состоять из таких цифр, чтобы каждая из них дополняла цифры в числах вашего оппонента до девяти. Если количество написанных чисел x, а количество цифр каждого числа — y, то искомую сумму находим по формуле x*(10y — 1). Если одно из чисел состоит из одних девяток, то дополнительного числа к нему приписывать не надо.
Для наглядности.
2545, 5674, 6784, 7640 (7454, 4325, 3215, 2359)
4*(104-1)=39996
5
ОПЯТЬ ПЯТЬ!

Наконец, пятый фокус. Его суть как раз в порядковом номере.
Предложите собеседнику загадать любое число,хоть семизначное (ему же сложнее будет, Вам — без разницы). После этого нужно прибавить к этому числу следующее по порядку число, а к нему прибавить девять. Далее — пусть поделит число на два и отнимет загаданное число. То число, которое получится, Вы легко угадаете. Это число будет пять.
Для наглядности. Пусть загаданное число будет 118.
1) 118+119=237
2) 237+9=246
3) 246:2=123
4) 123-118=5
Алексей Рудевич


Профилактика слабоумия
Когда вы последний раз включали свой мозг на полную?
Нагрузи свой мозг… по-разному!
Противопоказания
Где можно поиграть и позаниматься?
О себе

Итого
Трое математиков и трое физиков собираются ехать на поезде в другой город на конференцию. Они встречаются перед кассой на вокзале. Первой подходит очередь физиков и они, как все нормальные люди покупают по билету на человека. Математики же покупают один билет на всех. «Как же так?» — удивляются физики — «Ведь в поезде контроллер, вас же без билетов оттуда выгонят!». «Не волнуйтесь» — отвечают математики — «У нас есть МЕТОД».
Перед отправкой поезда физики рассаживаются по вагонам, но стараются проследить за применением загадочного «метода». Математики же все набиваются в один туалет. Когда контроллер подходит к туалету и стучит, дверь приотворяется, оттуда высовывается рука с билетом. Контроллер забирает билет и дальше все они без проблем едут в пункт назначения.
После конференции те же вновь встречаются на вокзале. Физики, воодушевившись примером математиков, покупают один билет. Математики не берут ни одного. — А что же вы покажете контроллеру? — У нас есть МЕТОД.
В поезде физики набиваются в один туалет, математики — в другой. Незадолго до отправления, один из математиков подходит к туалету, где прячутся физики. Стучит. Высовывается рука с билетом. Математик забирает билет и возвращается к коллегам.
МОРАЛЬ: Нельзя использовать математические методы не понимая их!
Математика и молодежь. Математик Армен Сергеев о привлечении новых кадров в математику, популяризации науки в СССР и институтах принстонского типа.
Как заинтересовать молодежь математической наукой? Для чего необходимо создание новых научных центров? Готовы ли уехавшие ученые способствовать развитию российской математики? Об этом рассказывает доктор физико-математических наук Армен Сергеев.

Максим Концевич
Лауреатами ежегодной Breakthrough Prize в области математики стали французский ученый российского происхождения Максим Концевич, англичане Саймон Дональдсон и Ричард Тейлор, американо-австралийский ученый китайского происхождения Теренс Тао и американец Джейкоб Лурье. Об этом в интервью «Газете.Ru» сообщил один из сооснователей премии Юрий Мильнер. Каждый ее лауреат получает три миллиона долларов, что делает Breakthrough Prize крупнейшей по размеру премиальных научной наградой.
Премию Концевичу присудили за работы в области алгебраической геометрии, теории деформаций, симплектической топологии, гомологической алгебры и теории динамических систем. Официальное заявление о присуждении премии состоится в Сан-Франциско утром в понедельник по местному времени.
Ранее, в 2012 году, Концевич стал лауреатом премии Fundamental Prize по физике. Эту награду, соучредителем которой также является Мильнер, ученый получил за вклад в современную математическую физику, а именно разработку гомологической зеркальной симметрии и исследования явлений узлов пересечений стены. На сегодняшний момент Концевич занимает должность постоянного профессора в Институте высших научных исследований в Бюр-сюр-Иветт под Парижем.
Премия Breakthrough Prize учреждена Юрием Мильнером, совладельцем Mail.ru Group, и Марком Цукербергом, генеральным директором и одним из основателей Facebook. С 2013 года премия ежегодно присуждается в области исследований продолжительности человеческой жизни, биомедицины и наук о жизни. Вручение премии в области математики состоится впервые.
Источник






