Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Золотое сечение – гармоническая пропорция

В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b = c : d.

Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a : b = b : c или с : b = b : а.

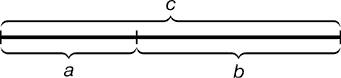
Рис. 1. Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

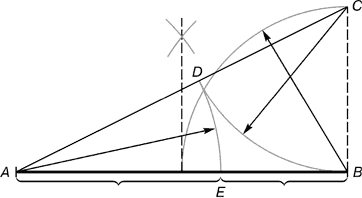
Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x2 – x – 1 = 0.

Решение этого уравнения:

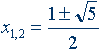
Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
Второе золотое сечение

Болгарский журнал «Отечество» (№10, 1983 г.) опубликовал статью Цветана Цекова-Карандаша «О втором золотом сечении», которое вытекает из основного сечения и дает другое отношение 44 : 56.

Такая пропорция обнаружена в архитектуре, а также имеет место при построении композиций изображений удлиненного горизонтального формата.

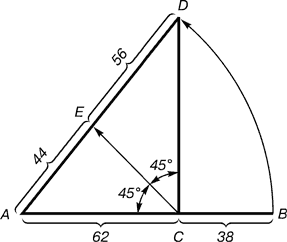
Рис. 3. Построение второго золотого сечения

Деление осуществляется следующим образом. Отрезок АВ делится в пропорции золотого сечения. Из точки С восставляется перпендикуляр СD. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой угол АСD делится пополам. Из точки С проводится линия до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56 : 44.

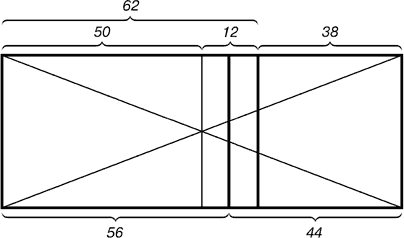
Рис. 4. Деление прямоугольника линией второго золотого сечения

На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.
Золотой треугольник

Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.

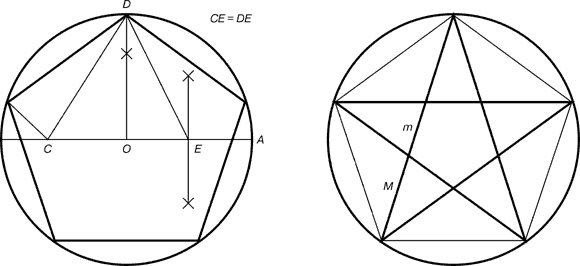
Рис. 5. Построение правильного пятиугольника и пентаграммы

Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

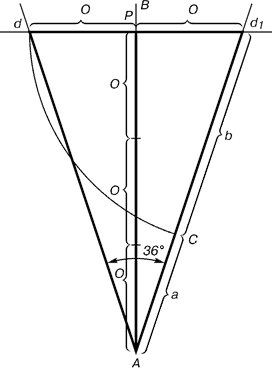
Рис. 6. Построение золотого
треугольника

Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.

История золотого сечения

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

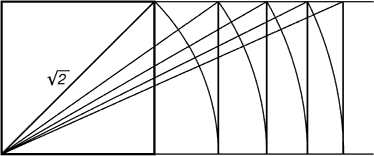
Рис. 7. Динамические прямоугольники

Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

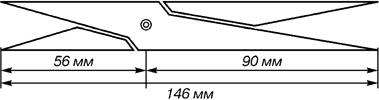
Рис. 8. Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

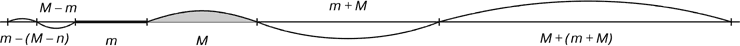
Рис. 9. Построение шкалы отрезков золотой пропорции

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

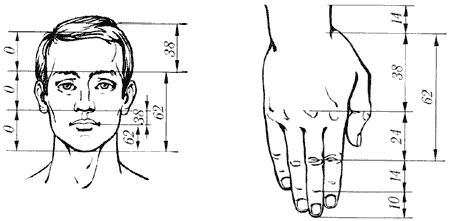
Рис. 10. Золотые пропорции в частях тела человека

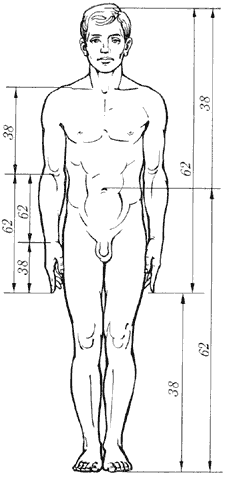
Рис. 11. Золотые пропорции в фигуре человека

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.

В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.
Ряд Фибоначчи

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Месяцы 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д.
Пары кроликов 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…
Обобщенное золотое сечение

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого сечения. Ю. Матиясевич с использованием чисел Фибоначчи решает 10-ю проблему Гильберта. Возникают изящные методы решения ряда кибернетических задач (теории поиска, игр, программирования) с использованием чисел Фибоначчи и золотого сечения. В США создается даже Математическая Фибоначчи-ассоциация, которая с 1963 года выпускает специальный журнал.

Одним из достижений в этой области является открытие обобщенных чисел Фибоначчи и обобщенных золотых сечений.

Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и открытый им же «двоичный» ряд гирь 1, 2, 4, 8, 16… на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2…, во втором – это сумма двух предыдущх чисел 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2…. Нельзя ли отыскать общую математическую формулу, из которой получаются и «двоичный» ряд, и ряд Фибоначчи? А может быть, эта формула даст нам новые числовые множества, обладающие какими-то новыми уникальными свойствами?

Действительно, зададимся числовым параметром S, который может принимать любые значения: 0, 1, 2, 3, 4, 5… Рассмотрим числовой ряд, S + 1 первых членов которого – единицы, а каждый из последующих равен сумме двух членов предыдущего и отстоящего от предыдущего на S шагов. Если n-й член этого ряда мы обозначим через φS (n), то получим общую формулу φS (n) = φS (n – 1) + φS (n – S – 1).

Очевидно, что при S = 0 из этой формулы мы получим «двоичный» ряд, при S = 1 – ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.

В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1 = 0.

Нетрудно показать, что при S = 0 получается деление отрезка пополам, а при S = 1 –знакомое классическое золотое сечение.

Отношения соседних S-чисел Фибоначчи с абсолютной математической точностью совпадают в пределе с золотыми S-пропорциями! Математики в таких случаях говорят, что золотые S-сечения являются числовыми инвариантами S-чисел Фибоначчи.

Факты, подтверждающие существование золотых S-сечений в природе, приводит белорусский ученый Э.М. Сороко в книге «Структурная гармония систем» (Минск, «Наука и техника», 1984). Оказывается, например, что хорошо изученные двойные сплавы обладают особыми, ярко выраженными функциональными свойствами (устойчивы в термическом отношении, тверды, износостойки, устойчивы к окислению и т. п) только в том случае, если удельные веса исходных компонентов связаны друг с другом одной из золотых S-пропорций. Это позволило автору выдвинуть гипотезe о том, что золотые S-сечения есть числовые инварианты самоорганизующихся систем. Будучи подтвержденной экспериментально, эта гипотеза может иметь фундаментальное значение для развития синергетики – новой области науки, изучающей процессы в самоорганизующихся системах.

С помощью кодов золотой S-пропорции можно выразить любое действительное число в виде суммы степеней золотых S-пропорций с целыми коэффициентами.

Принципиальное отличие такого способа кодирования чисел заключается в том, что основания новых кодов, представляющие собой золотые S-пропорции, при S > 0 оказываются иррациональными числами. Таким образом, новые системы счисления с иррациональными основаниями как бы ставят «с головы на ноги» исторически сложившуюся иерархию отношений между числами рациональными и иррациональными. Дело в том, что сначала были «открыты» числа натуральные; затем их отношения – числа рациональные. И лишь позже – после открытия пифагорийцами несоизмеримых отрезков – на свет появились иррациональные числа. Скажем, в десятичной, пятеричной, двоичной и других классических позиционных системах счисления в качестве своеобразной первоосновы были выбраны натуральные числа – 10, 5, 2, – из которых уже по определенным правилам конструировались все другие натуральные, а также рациональные и иррациональные числа.

Своего рода альтернативой существующим способам счисления выступает новая, иррациональная система, в качестве первоосновы, начала счисления которой выбрано иррациональное число (являющееся, напомним, корнем уравнения золотого сечения); через него уже выражаются другие действительные числа.

В такой системе счисления любое натуральное число всегда представимо в виде конечной – а не бесконечной, как думали ранее! – суммы степеней любой из золотых S-пропорций. Это одна из причин, почему «иррациональная» арифметика, обладая удивительной математической простотой и изяществом, как бы вобрала в себя лучшие качества классической двоичной и «Фибоначчиевой» арифметик.
Принципы формообразования в природе

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.

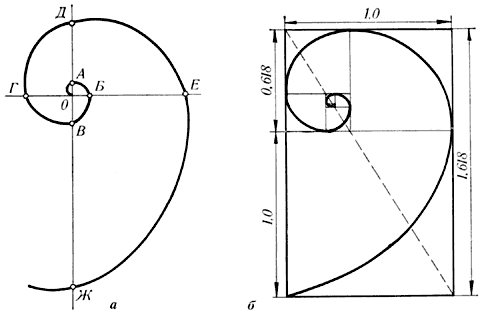
Рис. 12. Спираль Архимеда

Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

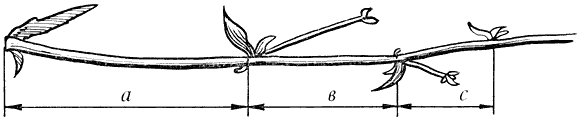
Рис. 13. Цикорий

Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

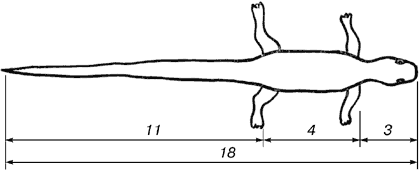
Рис. 14. Ящерица живородящая

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

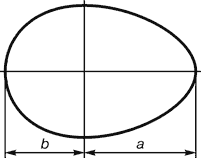
Рис. 15. Яйцо птицы

Великий Гете, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввел в научный обиход термин морфология.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
Золотое сечение и симметрия

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863…1925) считал золотое сечение одним из проявлений симметрии.

Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Источники информации:
Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
Кеплер И. О шестиугольных снежинках. – М., 1982.
Дюрер А. Дневники, письма, трактаты – Л., М., 1957.
Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
Стахов А. Коды золотой пропорции.